��Ŀ����
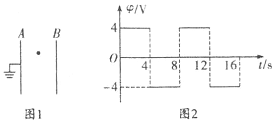
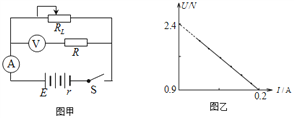
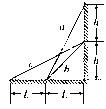
����Ŀ����ͼ��ʾ����ֱƽ�������ķ�֮һԲ������̶���ˮƽ�����ϣ�Բ��ΪO�㣮һС������Բ�����A���ɾ�ֹ��ʼ���ɻ��£���B����ˮƽ����ɳ����䵽ˮƽ����C�㣮��֪С���������Ϊm=1.0kg��C����B���ˮƽ����Ϊ1.0m��B��߶�Ϊ1.25m��Բ������뾶R=1.0m��ȡg=10m/s2����С���飺

��1����B��ɳ�ʱ���ٶȴ�С��
��2����B��ʱ��Բ�������ѹ����С��
��3����Բ������»������п˷�Ħ���������Ĺ���
���𰸡���1����B��ɳ�ʱ���ٶȴ�СΪ2m/s��
��2����B��ʱ��Բ�������ѹ����С��14N��
��3����Բ������»������п˷�Ħ���������Ĺ���8J��
�������������������1�������B��ɳ�����ƽ���˶������B��ɳ�ʱ���ٶȴ�СΪv������
��ֱ����h=![]() gt2
gt2
ˮƽ����x=vt
��� v=2m/s
��2�����龭��B��ʱ�������������֧�����ĺ����ṩ����������ţ�ٵڶ����ɵ�
![]()
��� N=14N
����ţ�ٵ������ɵã���B��ʱ�����Բ�������ѹ����СΪN��=N=14N��������ֱ���£�
��3������Բ������»������л���˷�Ħ���������Ĺ�ΪW���ɶ��ܶ�����
mgR-W=![]() mv2
mv2
��� W=8J

��ϰ��ϵ�д�
 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
�����Ŀ