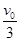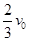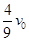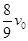题目内容
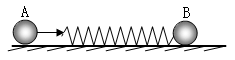
如图所示,光滑水平面上的木板右端,有一根轻质弹簧沿水平方向与木板相连,木板质量M=3.0kg。质量m=1.0kg的铁块以水平速度 =4.0m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.则在上述过程中弹簧具有的最大弹性势能为
=4.0m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.则在上述过程中弹簧具有的最大弹性势能为
| A.3.0J | B.4.0J | C.6.0J | D.20J |
A
解析试题分析:据题意,当m向右运动过程中,由于摩擦力作用,m做减速运动,M做加速运动,压缩弹簧过程也是由于弹力作用,继续类似运动,知道两者速度相等时,弹簧压缩到最短,设此时速度为v1,据动量守恒定律有: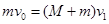 ,计算得:
,计算得: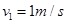 ,此后m在弹力作用下减速运动M加速运动,离开弹簧后在摩擦力作用下,m做加速运动而M作减速运动,知道两者速度相等时相等静止,设此时速度为v2,据动量守恒定律有:
,此后m在弹力作用下减速运动M加速运动,离开弹簧后在摩擦力作用下,m做加速运动而M作减速运动,知道两者速度相等时相等静止,设此时速度为v2,据动量守恒定律有: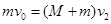 ,计算得:
,计算得: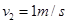 ,则m从左端运动到把弹簧压缩到最短过程中有据能量守恒定律有:
,则m从左端运动到把弹簧压缩到最短过程中有据能量守恒定律有: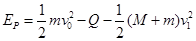 ,m从左端运动到再次回到左端过程中据能量守恒定律有:
,m从左端运动到再次回到左端过程中据能量守恒定律有: ,最后计算得最大弹性势能为3J,则A选项正确。
,最后计算得最大弹性势能为3J,则A选项正确。
考点:本题考查动量守恒定律和能量守恒定律的应用。

小孩双手搭着大人的肩一起在水平冰面上以3m/s的速度向右匀速滑行,后面的小孩突然推了一下前面的大人,结果小孩以2m/s的速度向左滑行,已知小孩的质量为30kg,大人的质量为60kg,则被推后大人的速度大小变为___________。(填选项前的字母)
| A.5.5m/s | B.4.5m/s | C.3.5m/s | D.2.5m/s |
质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ。初始时小物块停在箱子正中间,如图所示。现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,井与箱子保持相对静止。设碰撞都是弹性的,则整个过程中,系统损失的动能为 
A. | B. | C.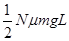 | D.(N-1)μmgL |
质量相等的三个物体在一光滑水平面上排成一直线,且彼此隔开一定距离,如图,具有初动能E0的第一号物块向右运动,依次与其余两个物块发生碰撞,最后这三个物体粘成一个整体,这个整体的动能等于
| A.E0 | B. 2E0/3 | C. E0/3 | D. E0/9 |

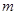 的小球A在光滑的水平面上以速度
的小球A在光滑的水平面上以速度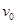 与质量为
与质量为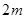 的静止小球B发生正碰,碰后A球的动能恰好变为原来的
的静止小球B发生正碰,碰后A球的动能恰好变为原来的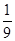 ,则B球速度大小可能是( )
,则B球速度大小可能是( )