题目内容
如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙壁。重物质量为木板质量的两倍,重物与木板间的动摩擦因数为µ。使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求木板从第一次与墙壁碰撞到再次与重物速度相同时,木板右端离墙壁的距离。
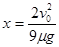
解析试题分析:设木板质量为m,重物质量为2m,取向右为正方向,由动量守恒得:
2mv0-mv0=3mv 2分
设从第一次与墙壁碰撞到重物和木板具有共同速度v所用时间为t,对木板由动量定理得:
2µmgt=mv-m(-v0)
对木板由牛顿第二定律得
-2µmg=ma
木板从第一次与墙壁碰撞到再次与重物速度相同时,木板右端离墙壁的距离为:
x=v0t+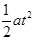
解得: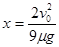
考点: 动量守恒定律应用;动量定理

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
下面的说法正确的是( )
| A.物体运动的方向就是它的动量的方向 |
| B.如果物体的速度发生变化,则可以肯定它受到的合外力的冲量不为零 |
| C.如果合外力对物体的冲量不为零,则合外力一定使物体的动能增大 |
| D.作用在物体上的合外力冲量不一定能改变物体速度的大小 |

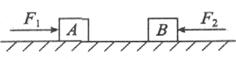

 (相对空间站)将物体A推出
(相对空间站)将物体A推出 ,求甲与A的相互作用力F的大小
,求甲与A的相互作用力F的大小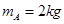 、物块B的质量为
、物块B的质量为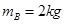 ,开始都静止在光滑水平面上,现用大小均为F=5N的两个力分别作A和B上,使A、B沿一条直线相向运动,物块A上的力作用时间为
,开始都静止在光滑水平面上,现用大小均为F=5N的两个力分别作A和B上,使A、B沿一条直线相向运动,物块A上的力作用时间为 ,物块B上的力作用时问为
,物块B上的力作用时问为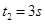 ,先后撤去这两个力后两物块发生对心正碰。如果碰撞后两个物块粘合为一体,求其运动的速度。
,先后撤去这两个力后两物块发生对心正碰。如果碰撞后两个物块粘合为一体,求其运动的速度。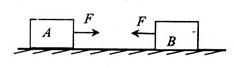
 =4.0m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.则在上述过程中弹簧具有的最大弹性势能为
=4.0m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.则在上述过程中弹簧具有的最大弹性势能为