Question

如图所示，用长为l的绝缘细线拴一个质量为m、带电量为＋q的小球(可视为质点)后悬挂于O点，整个装置处于水平向右的匀强电场E中．将小球拉至使悬线呈水平的位置A后，由静止开始将小球释放，小球从A点开始向下摆动，当悬线转过60°角到达位置B时，速度恰好为零．求：

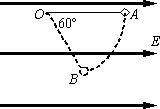
(1)B、A两点的电势差U_BA；

(2)电场强度E；

(3)小球到达B点时，悬线对小球的拉力T．

Answer 1

答案：
解析：

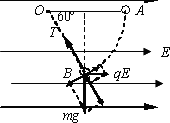
解．(1)根据动能定理： 　　mglsin60°－qUBA＝0－0，B、A两点的电势差(4分) 　　(2)电场强度(4分) 　　(3)小球到达B点时，悬线对小球的拉力T、重力沿半径方向的分力mgcos30°、电场力沿半径方向的分力qEcos60°的合力是向心力： 　　 　　因为vB＝0， 　　解得T＝mg．(4分)