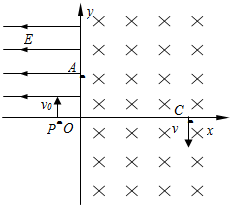
题目内容
如图所示,一矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(ab、dc边足够长),现从矩形区域ad边的中点O处,垂直磁场射入一速度方向与ad边夹角为30°、大小为v0的带正电粒子,已知粒子质量为m,电荷量为q,ad边长为l,重力影响不计,要使粒子从ab边上射出磁场,则( )

A.只要粒子的速度小于
| ||||
B.只要粒子的速度大于
| ||||
C.只要粒子的速度小于
| ||||
D.速度在
|

(1)粒子带正电,粒子运动的轨迹如图所示,当粒子的速度不大于与R1相对应的速度v1时,粒子将恰好不从dc边射出.
由几何关系可得:R1=L…①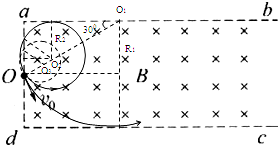
由洛仑兹力和向心力公式可得:qv1B=
… ②
当粒子的速度小于与R2相对应的速度v2时,粒子将从ad边射出.
由几何关系可得:R2+R2sin30°=
L…③
由③式解得:R2=
L…④
由洛仑兹力和向心力公式可得:qv2B=
…⑤
将①④式分别代入②⑤式可解得:v1=
;v2=
…⑥
所以v0的取值范围是:
<v<
…⑦
故选:D
由几何关系可得:R1=L…①

由洛仑兹力和向心力公式可得:qv1B=
m
| ||
| R1 |
当粒子的速度小于与R2相对应的速度v2时,粒子将从ad边射出.
由几何关系可得:R2+R2sin30°=
| 1 |
| 2 |
由③式解得:R2=
| 1 |
| 3 |
由洛仑兹力和向心力公式可得:qv2B=
m
| ||
| R2 |
将①④式分别代入②⑤式可解得:v1=
| qBL |
| m |
| qBL |
| 3m |
所以v0的取值范围是:
| qBL |
| 3m |
| qBL |
| m |
故选:D

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目