��Ŀ����
����Ŀ�����϶���������·��и߶���100 km�������϶�һ���������������100 km�����һ�Ҫ��ε�������100 km��15 km����Բ������У��������϶���������µ�Բ�����Ϊ��������������߶���Ϊh1����Բ�����Ϊ������ص����������ĸ߶���Ϊh2����ͼ��ʾ�����������������ٶ���Ϊg0������뾶��ΪR.��

��1�����϶�������ڹ�����ϵ��������ʣ�
��2�������϶�������ڹ�����Ϸ��У���A�㴦�����������ɣ�������α仯��
��3�������϶�������ع�������У�������ǽ��¹��������Ϊ���ٶȴ�С���䣬��Ϊg0��A����ٶ���֪ΪvA�������϶���������е�B����ٶȣ�
���𰸡�(1) 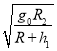 (2) ���ܼ��� (3)
(2) ���ܼ��� (3) ![]() ��
��![]()
�������������������Ҫ����Բ���˶�����������ʽ������������ʽ�ı任��ͨ���������ʽ����������ʣ������������պ��ṩ��������������ʱ �������ÿ���������Բ���˶������ǹ������� ������������Բ�ĵ��˶������ǹ�С��������������Զ��Բ�ĵ��˶������ݻ�е���غ�ɵ����϶���������е�B����ٶȡ�
��1������������ΪM�����϶������������Ϊm��
�������������ṩ�������� 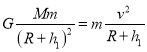
������������������������� ![]()
��ã� 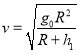
��2�����϶�������ڰ뾶Ϊh1��Բ�ι�����˶�����������A��ʱ����������Բ����������������ĵ��˶���Ҫʵ������˶����������������ڷɴ�����������������Ӧ���ɴ����٣���С����������������Էɴ���A�㴦���ʱ���ܼ�С��
��3���ڹ�����ϣ���A��B�����У�
��е���غ�ɵã� ![]()
����� ![]() ���ɿ����ն��ɽ����
���ɿ����ն��ɽ���� ![]()

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�




