��Ŀ����
20�� ��ͼ��ʾΪij�������ĸֶ�����װ�ã�б�³�ΪL=20m����Ϊh=2m��б���Ͻ�����һ�Ź�Ͳ����Ϊl=8m������Ϊm=1��103kg�ĸֶ�ab���ڹ�Ͳ�ϣ��ֶ����Ͳ��Ķ�Ħ������Ϊ��=0.3������ʱ�ɵ綯���������й�Ͳ˳ʱ������ת����ʹ�ֶ���б�������ƶ�����Ͳ��Ե�����ٶȾ�Ϊv=4m/s������رյ綯����˲ʱ���й�Ͳ����ֹͣת�����ֶ��Թ�Ͳ����ѹ���Ĵ�С���Ƶ��ڸֶ���������ȡ���ص��������ٶ�g=10m/s2������
��ͼ��ʾΪij�������ĸֶ�����װ�ã�б�³�ΪL=20m����Ϊh=2m��б���Ͻ�����һ�Ź�Ͳ����Ϊl=8m������Ϊm=1��103kg�ĸֶ�ab���ڹ�Ͳ�ϣ��ֶ����Ͳ��Ķ�Ħ������Ϊ��=0.3������ʱ�ɵ綯���������й�Ͳ˳ʱ������ת����ʹ�ֶ���б�������ƶ�����Ͳ��Ե�����ٶȾ�Ϊv=4m/s������رյ綯����˲ʱ���й�Ͳ����ֹͣת�����ֶ��Թ�Ͳ����ѹ���Ĵ�С���Ƶ��ڸֶ���������ȡ���ص��������ٶ�g=10m/s2��������1���ֶ����µף���ͼ��ʾλ�ã��ɾ�ֹ��ʼ�˶���ֱ��b�˵����¶���������ʱ�䣮
��2���ֶ����µף���ͼ��ʾλ�ã��ɾ�ֹ��ʼ�˶���ֱ��b�˵����¶��Ĺ����е綯������Ҫ�����ʱ�䣿
���� ��1����ʹb�˵����¶�����Ҫ��ʱ����̣���Ҫ�綯��һֱ��������ֹ������ȼ���ֱ���˶����������ٶȵ��ڹ�Ͳ��Ե�����ٶȺ�������ֱ���˶���
��2����ʹ�綯��������ʱ����̣��ֹ�����һ���˶�Ҫ�رյ綯�����ֹ��ȼ������������ֹ��ȼ��ٺ����٣������٣��ʵ������ʱ����ڳ�ȥ������ֹ���˶�ʱ�䣮
��� �⣺��1���ֶ���ʼ�ܵ��Ļ���Ħ����Ϊ��f1=��mg=3��103N��
��б����ˮƽ��ļн�Ϊ������ţ�ٵڶ������У�Ff-mgsin��=ma1��
�������ݽ�ã�${a_1}=2m/{s^2}$��
�ֶ����ȼ����˶���ʱ�䣺${t_1}=\frac{v}{a}=2s$��λ�ƣ�${x_1}=\frac{1}{2}{a_1}t_1^2=4m$��
Ҫʹb�˵����¶�����Ҫ��ʱ����̣���Ҫ�綯��һֱ�������ֶ������ȼ���ֱ���˶���
�������ٶȵ��ڹ�Ͳ��Ե�����ٶȺ�������ֱ���˶����ֶ�������ֱ���˶���λ�ƣ�
x2=L-l-x1=8m��������ֱ���˶���ʱ�䣺${t_2}=\frac{x_2}{v}=2s$��
�������ʱ�� t=t1+t2=4s��
��2��Ҫʹ�綯������ʱ����̣��ֶ������һ���˶�Ҫ�رյ綯����
�ֶ��ȼ���������b�˵����¶�ʱ�ٶȸպ�Ϊ�㣮
�ȼ�������ʱ����ţ�ٵڶ����ɵã�Ff+mgsin��=ma2��
�������ݽ�ã�${a_2}=4m/{s^2}$��
�ȼ����˶�ʱ�䣺${t_3}=\frac{v}{a_2}=1s$��
�ȼ����˶�λ�ƣ�${x_3}=\frac{v}{2}{t_3}=2m$��
�����˶���λ�ƣ�x4=L-l-x1-x3=6m��
�綯������Ҫ������ʱ�䣺$t={t_1}+\frac{x_4}{v}=3.5s$��
�𣺣�1���ֶ����µף���ͼ��ʾλ�ã��ɾ�ֹ��ʼ�˶���ֱ��b�˵����¶���������ʱ����4s��
��2���ֶ����µף���ͼ��ʾλ�ã��ɾ�ֹ��ʼ�˶���ֱ��b�˵����¶��Ĺ����е綯������Ҫ����3.5s��
���� ����ؼ�����ȷ�ֹ���˶����ɣ�Ȼ��ֽθ���ţ�ٵڶ����������ٶȣ��ٸ����˶�ѧ��ʽ��ʽ��⣮

| A�� | 5W | B�� | 10W | C�� | 50W | D�� | 100W |
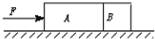 ��ͼ��ʾ������Ϊ2kg�����A��ˮƽ����Ķ�Ħ������Ϊ��=0.1������1kg�����B������Ħ�����Բ��ƣ�����֪ˮƽ��F=11N�������£�A��Bһ���������˶���������˵������ȷ���ǣ�������
��ͼ��ʾ������Ϊ2kg�����A��ˮƽ����Ķ�Ħ������Ϊ��=0.1������1kg�����B������Ħ�����Բ��ƣ�����֪ˮƽ��F=11N�������£�A��Bһ���������˶���������˵������ȷ���ǣ�������| A�� | AB�ļ��ٶȾ�Ϊ3.0m/s2 | B�� | AB�ļ��ٶȾ�Ϊ3.3m/s2 | ||
| C�� | A��B��������Ϊ3.3N | D�� | A��B��������Ϊ3.0N |
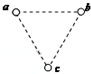 ��ͼ���ڹ⻬��Եˮƽ���ϣ����������ʵ�a��b��c�ֱ�λ�ڱ߳�ΪL���������ε����������ϣ�a��b�������Ϊq��Ϊͬ�ֵ�ɣ�����ϵͳ����ˮƽ�������ǿ�糡�У���֪����������Ϊk���������ʵ�����ھ�ֹ״̬��������˵����ȷ���ǣ�������
��ͼ���ڹ⻬��Եˮƽ���ϣ����������ʵ�a��b��c�ֱ�λ�ڱ߳�ΪL���������ε����������ϣ�a��b�������Ϊq��Ϊͬ�ֵ�ɣ�����ϵͳ����ˮƽ�������ǿ�糡�У���֪����������Ϊk���������ʵ�����ھ�ֹ״̬��������˵����ȷ���ǣ�������| A�� | ���a��b�����磬��ôcһ�������� | B�� | ��ǿ�糡��ǿ�Ĵ�СΪ$\frac{\sqrt{3}kq}{{l}^{2}}$ | ||
| C�� | �ʵ�c�ĵ�����СΪ$\sqrt{2}$q | D�� | ��ǿ�糡�ķ�����ab�ߴ�ֱ����c |

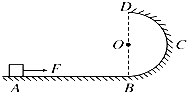 ��ͼ10��ʾ��ˮƽ���AB��λ����ֱ���ڰ뾶ΪR=0.90 m�İ�Բ�ι⻬���BCD��������Բ�ι����BD������AB��ֱ������Ϊm=1.0kg�ɿ����ʵ��С�����ں㶨����F�����´�ˮƽ����ϵ�A���ɾ�ֹ��ʼ�����˶���������ˮƽ���AB��Ķ�Ħ������ ��=0.5������ˮƽ�����ĩ��B��ʱ��ȥ��������������ذ�Բ�ι���˶�����ǡ����ͨ�������ߵ�D�����������Բ�ι�����ָպ��䵽A�㣮gȡ10m/s2����
��ͼ10��ʾ��ˮƽ���AB��λ����ֱ���ڰ뾶ΪR=0.90 m�İ�Բ�ι⻬���BCD��������Բ�ι����BD������AB��ֱ������Ϊm=1.0kg�ɿ����ʵ��С�����ں㶨����F�����´�ˮƽ����ϵ�A���ɾ�ֹ��ʼ�����˶���������ˮƽ���AB��Ķ�Ħ������ ��=0.5������ˮƽ�����ĩ��B��ʱ��ȥ��������������ذ�Բ�ι���˶�����ǡ����ͨ�������ߵ�D�����������Բ�ι�����ָպ��䵽A�㣮gȡ10m/s2����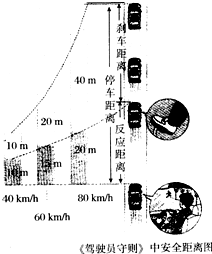 ��ʻԱ��������·���ˣ��Ӿ���ͣ����ֱ���ҽŸող����ƶ���̤���Ͼ�����ʱ�䣬�з�Ӧʱ�䣻�ڷ�Ӧʱ���ڣ�������һ���ٶ���ʻ�ľ����Ϊ��Ӧ���룬�ӲȽ�̤�嵽��ͣ�µ���ξ����Ϊɲ�����룬˾���ӷ��������������ȫͣ������������ͨ���ľ������ͣ�����룬��ͼ��ʾ����ij˾���ķ�Ӧʱ��Ϊt����ͣ������Ϊs���������������ʻʱ���ٶ�Ϊvo��ɲ���ƶ����Ƕ�ֵf����������Ϊm�����������˾���ӷ��������������ȫֹͣ��һʵ���龳���Ƴ�ͣ������s�ı���ʽ��s=v0t0+$\frac{mv_0^2}{2f}$��
��ʻԱ��������·���ˣ��Ӿ���ͣ����ֱ���ҽŸող����ƶ���̤���Ͼ�����ʱ�䣬�з�Ӧʱ�䣻�ڷ�Ӧʱ���ڣ�������һ���ٶ���ʻ�ľ����Ϊ��Ӧ���룬�ӲȽ�̤�嵽��ͣ�µ���ξ����Ϊɲ�����룬˾���ӷ��������������ȫͣ������������ͨ���ľ������ͣ�����룬��ͼ��ʾ����ij˾���ķ�Ӧʱ��Ϊt����ͣ������Ϊs���������������ʻʱ���ٶ�Ϊvo��ɲ���ƶ����Ƕ�ֵf����������Ϊm�����������˾���ӷ��������������ȫֹͣ��һʵ���龳���Ƴ�ͣ������s�ı���ʽ��s=v0t0+$\frac{mv_0^2}{2f}$��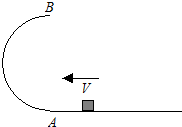 ����ֱƽ������һ�뾶ΪR�Ĺ⻬��Բ�ι̶����������͵�A��ˮƽ�����У�һ����Ϊm��������͵���ijһ�ٶȳ��Ϲ����������ߵ�Bʱ�Ͱ�Բ���֮����������Ĵ�СΪmg����
����ֱƽ������һ�뾶ΪR�Ĺ⻬��Բ�ι̶����������͵�A��ˮƽ�����У�һ����Ϊm��������͵���ijһ�ٶȳ��Ϲ����������ߵ�Bʱ�Ͱ�Բ���֮����������Ĵ�СΪmg����