题目内容
12.雨滴在穿过云层的过程中,不断与漂浮在云层中的小水珠相遇并结合为一体,其质量逐渐增大.现将上述过程简化为沿竖直方向的一系列碰撞.已知雨滴的初始质量为m0,初速度为v0,下降距离l后与静止的小水珠碰撞且合并,质量变为m1.此后每经过同样的距离l后,雨滴均与静止的小水珠碰撞且合并,质量依次变为m2、m3…mm…(设各质量为已知量).不计空气阻力.(1)若不计重力,求第n次碰撞后雨滴的速度vn;
(2)若考虑重力的影响,
a.求第1次碰撞前、后雨滴的速度v1和v1;
b.求第n次碰撞后雨滴的动能$\frac{1}{2}$mnv′n2.
分析 (1)忽略重力与阻力,系统所受合外力为零,动量守恒,由动量守恒定律可以求出速度.
(2)碰撞过程系统动量守恒,应用匀变速运动的速度位移公式与动量守恒定律可以求出速度,然后求出动能.
解答 解:(1)不计重力,全过程中动量守恒,以向下为正方向,由动量守恒定律得:
m0v0=mnvn′,
解得:vn′=$\frac{{m}_{0}{v}_{0}}{{m}_{n}}$;
(2)若考虑重力的影响,雨滴下降过程中做加速度为g的匀加速运动,碰撞瞬间动量守恒,以向下为正方向,a、第1次碰撞前,由匀变速运动的速度位移公式得:
v12-v02=2gl,
解得:v1=$\sqrt{{v}_{0}^{2}+2gl}$,
第1次碰撞过程,由动量守恒定律得:m0v1=m1v1′,
解得:v1′=$\frac{{m}_{0}}{{m}_{1}}\sqrt{{v}_{0}^{2}+2gl}$;
b.第2次碰撞前:v22-v1′2=2gl,
解得:v22=($\frac{{m}_{0}}{{m}_{1}}$)2v02+($\frac{{m}_{0}^{2}+{m}_{1}^{2}}{{m}_{1}^{2}}$)2gl,
第2次碰撞过程,由动量守恒定律得:m1v2=m2v2′,
解得:v2′2=($\frac{{m}_{0}}{{m}_{2}}$)2v02+($\frac{{m}_{0}^{2}+{m}_{1}^{2}}{{m}_{2}^{2}}$)2gl,
同理,第3次碰撞后:v3′2=($\frac{{m}_{0}}{{m}_{3}}$)2v02+($\frac{{m}_{0}^{2}+{m}_{1}^{2}+{m}_{2}^{2}}{{m}_{3}^{2}}$)2gl,
…
第n次碰撞后,vn′2=($\frac{{m}_{0}}{{m}_{n}}$)2v02+($\frac{\sum_{i=0}^{n-1}{m}_{i}^{2}}{{m}_{n}^{2}}$)2gl,
动能:EK=$\frac{1}{2}$mnvn′2=$\frac{1}{2{m}_{n}}$(m02v02+2gl$\frac{\sum_{i=0}^{n-1}{m}_{i}^{2}}{{m}_{n}^{2}}$);
答:(1)若不计重力,求第n次碰撞后雨滴的速度vn′=$\frac{{m}_{0}{v}_{0}}{{m}_{n}}$;
(2)若考虑重力的影响,a.求第1次碰撞前、后雨滴的速度v1=$\sqrt{{v}_{0}^{2}+2gl}$,v1′=$\frac{{m}_{0}}{{m}_{1}}\sqrt{{v}_{0}^{2}+2gl}$;
b.求第n次碰撞后雨滴的动能EK=$\frac{1}{2{m}_{n}}$(m02v02+2gl$\frac{\sum_{i=0}^{n-1}{m}_{i}^{2}}{{m}_{n}^{2}}$).
点评 本题考查了求雨滴的速度与动能问题,分析清楚运动过程,应用动量守恒定律、匀变速运动的速度位移公式即可正确解题,解题时注意数学知识的应用.

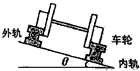 铁路在弯道处的内外轨道高度是不同的,已知内外轨道所在平面与水平面成θ,如图所示,水平弯道处的圆弧半径为R,若质量为m的火车以大于$\sqrt{Rgtanθ}$的速度匀速率转弯时,下列说法正确的是( )
铁路在弯道处的内外轨道高度是不同的,已知内外轨道所在平面与水平面成θ,如图所示,水平弯道处的圆弧半径为R,若质量为m的火车以大于$\sqrt{Rgtanθ}$的速度匀速率转弯时,下列说法正确的是( )| A. | 内轨对内侧车轮轮缘有挤压 | |
| B. | 外轨对外侧车轮轮缘有挤压R | |
| C. | 这时铁轨对火车的支持力等于$\frac{mg}{cosθ}$ | |
| D. | 这时铁轨对火车的作用力等于mgcosθ |
| A. | f=$\frac{1}{2}$F,Em=$\frac{Fs}{2}$ | B. | f=$\frac{1}{2}$F,Em=Fs | C. | f=$\frac{1}{3}$F,Em=$\frac{2Fs}{3}$ | D. | f=$\frac{2}{3}$F,Em=$\frac{1}{3}$Fs |
| A. | 地球绕太阳运动的周期及地球距太阳中心的距离 | |
| B. | 月球绕地球运动的周期及月球距地球中心的距离 | |
| C. | 人造卫星绕地球运动的速率 | |
| D. | 已知地球的半径和地球表面的重力加速度(不考虑地球自转的影响) |
| A. | 落地前瞬间,两小球的速度大小一定相同 | |
| B. | 从抛出到落地,重力对A、B小球做的功一样多 | |
| C. | 落地前瞬间,重力对两小球的瞬时功率一定相同 | |
| D. | 从抛出到落地,重力对两小球做的平均功率一定相同 |
 如图所示,物体P以一定的初速度v沿光滑水平面向右运动,与一个右端固定的轻质弹簧相撞,并被弹簧反向弹回,若弹簧在被压缩过程中始终遵守胡克定律,那么在P与弹簧发生相互作用的整个( )
如图所示,物体P以一定的初速度v沿光滑水平面向右运动,与一个右端固定的轻质弹簧相撞,并被弹簧反向弹回,若弹簧在被压缩过程中始终遵守胡克定律,那么在P与弹簧发生相互作用的整个( )| A. | P的加速度大小不断变化,方向也不断变化 | |
| B. | P的加速度大小不断变化,但方向不变 | |
| C. | P和弹簧组成的系统机械能守恒 | |
| D. | P的机械能的改变量小于弹簧对P所做的功 |
 如图所示为某钢铁厂的钢锭传送装置,斜坡长为L=20m,高为h=2m,斜坡上紧排着一排滚筒.长为l=8m、质量为m=1×103kg的钢锭ab放在滚筒上,钢锭与滚筒间的动摩擦因数为μ=0.3,工作时由电动机带动所有滚筒顺时针匀速转动,使钢锭沿斜坡向上移动,滚筒边缘的线速度均为v=4m/s.假设关闭电动机的瞬时所有滚筒立即停止转动,钢锭对滚筒的总压力的大小近似等于钢锭的重力.取当地的重力加速度g=10m/s2.试求:
如图所示为某钢铁厂的钢锭传送装置,斜坡长为L=20m,高为h=2m,斜坡上紧排着一排滚筒.长为l=8m、质量为m=1×103kg的钢锭ab放在滚筒上,钢锭与滚筒间的动摩擦因数为μ=0.3,工作时由电动机带动所有滚筒顺时针匀速转动,使钢锭沿斜坡向上移动,滚筒边缘的线速度均为v=4m/s.假设关闭电动机的瞬时所有滚筒立即停止转动,钢锭对滚筒的总压力的大小近似等于钢锭的重力.取当地的重力加速度g=10m/s2.试求: