题目内容
15．
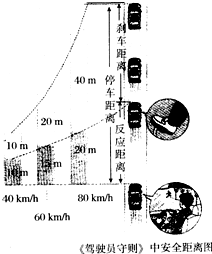驾驶员看见过马路的人，从决定停车，直至右脚刚刚踩在制动器踏板上经过的时间，叫反应时间；在反应时间内，汽车按一定速度行驶的距离称为反应距离，从踩紧踏板到车停下的这段距离称为刹车距离，司机从发现情况到汽车完全停下来，汽车所通过的距离叫做停车距离，如图所示．设某司机的反应时间为t．，停车距离为s．如果汽车正常行驶时的速度为vo，刹车制动力是定值f，汽车质量为m．请你就汽车司机从发现情况到汽车完全停止这一实际情境，推出停车距离s的表达式．s=v0t0+$\frac{mv_0^2}{2f}$．
分析 由匀速运动的位移公式求出反应距离，由牛顿第二定律求出刹车时的加速度，由速度位移求出刹车距离，然后求出停止距离．
解答 解：在反应时间内，汽车做匀速直线运动，位移：s1=v0t0，
刹车后，汽车做匀减速直线运动，由牛顿第二定律得：f=ma，
刹车距离：s2=$\frac{{{v}_{0}}^{2}}{2a}$，
停车距离：s=s1+s2=v0t0+$\frac{m{v}_{0}^{2}}{2f}$
故答案为：vs=0t0+$\frac{mv_0^2}{2f}$
点评 本题考查了求汽车的停车距离，分析清楚汽车的运动过程，应用运动学公式、牛顿第二定律即可正确解题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
3．木块在水平恒力F作用下沿水平路面由静止出发前进了s，随即撤去此恒力，木块又沿原方向前进了2s才停下来．设木块运动的全过程中地面情况相同，则摩擦力f和木块获得的最大动能Em为（ ）
| A． | f=$\frac{1}{2}$F，Em=$\frac{Fs}{2}$ | B． | f=$\frac{1}{2}$F，Em=Fs | C． | f=$\frac{1}{3}$F，Em=$\frac{2Fs}{3}$ | D． | f=$\frac{2}{3}$F，Em=$\frac{1}{3}$Fs |
如图所示为某钢铁厂的钢锭传送装置，斜坡长为L=20m，高为h=2m，斜坡上紧排着一排滚筒．长为l=8m、质量为m=1×103kg的钢锭ab放在滚筒上，钢锭与滚筒间的动摩擦因数为μ=0.3，工作时由电动机带动所有滚筒顺时针匀速转动，使钢锭沿斜坡向上移动，滚筒边缘的线速度均为v=4m/s．假设关闭电动机的瞬时所有滚筒立即停止转动，钢锭对滚筒的总压力的大小近似等于钢锭的重力．取当地的重力加速度g=10m/s2．试求：
4．有两个质量不同的小球A、B，从离地相同高度处以相同的速率分别沿水平方向和竖直向上方向抛出，不计空气阻力，则下列说法正确的是（ ）
| A． | 落地前瞬间，两小球的速度大小一定相同 | |
| B． | 从抛出到落地，重力对A、B小球做的功一样多 | |
| C． | 落地前瞬间，重力对两小球的瞬时功率一定相同 | |
| D． | 从抛出到落地，重力对两小球做的平均功率一定相同 |
如图所示，两根足够长、电阻不计的平行光滑金属导轨处于磁感应强度大小为B=0.5T的匀强磁场中，导轨平面与水平面成θ=30°角，下端连接“2.5V，0.5W”的小电珠，磁场方向与导轨平面垂直，质量为m=0.02kg、电阻不计的光滑金属棒与导轨垂直并保持良好接触，金属棒由静止开始释放，下滑速度达到稳定时，小电珠正常发光，取g=10m/s2，求：