题目内容
8.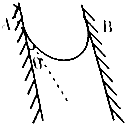 如图所示,一根柔软且均匀的绳子,两端系于竖直墙壁上的两个高度相同的悬点A、B上,绳子的质量为m,静止时绳子两端的切线方向与竖直墙壁的夹角为θ,求
如图所示,一根柔软且均匀的绳子,两端系于竖直墙壁上的两个高度相同的悬点A、B上,绳子的质量为m,静止时绳子两端的切线方向与竖直墙壁的夹角为θ,求(1)墙壁对绳子的拉力;
(2)绳子最低处的张力.
分析 对物体受力分析,受重力、水平拉力和天花板的拉力,物体保持静止,受力平衡,根据平衡条件并运用正交分解法列式求解即可.
解答 解:对物体受力分析,受重力、水平拉力和天花板的拉力,如图所示: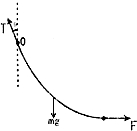
根据平衡条件,有
水平方向:F=Tsinθ
竖直方向:$\frac{1}{2}$mg=Tcosθ
联立解得:
T=$\frac{mg}{2cosθ}$
F=$\frac{1}{2}$mgtanθ
答:(1)墙壁对绳子的拉力为$\frac{mg}{2cosθ}$;
(2)绳子最低处的张力为$\frac{1}{2}$mgtanθ.
点评 本题关键是先对物体受力分析,然后根据平衡条件并运用正交分解法列式求解,对于三个不平行的力,若合力为零,一定是共点力.

练习册系列答案
相关题目
3.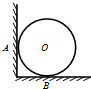 如图所示,一个光滑的球形物体O静止放在水平地面上,并与竖直墙相接触,A、B两点是球与墙和球与地面的接触点,则关于球形物所受弹力的个数为( )
如图所示,一个光滑的球形物体O静止放在水平地面上,并与竖直墙相接触,A、B两点是球与墙和球与地面的接触点,则关于球形物所受弹力的个数为( )
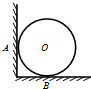 如图所示,一个光滑的球形物体O静止放在水平地面上,并与竖直墙相接触,A、B两点是球与墙和球与地面的接触点,则关于球形物所受弹力的个数为( )
如图所示,一个光滑的球形物体O静止放在水平地面上,并与竖直墙相接触,A、B两点是球与墙和球与地面的接触点,则关于球形物所受弹力的个数为( )| A. | 1 个 | B. | 2个 | C. | 3 个 | D. | 4个 |
18.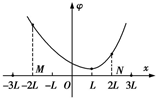 电荷量不等的两点电荷固定在x轴上坐标为-3L和3L的两点,其中坐标为3L处电荷带正电,电荷量为Q.两点电荷连线上各点电势φ随x变化的关系如图所示,其中x=L处电势最低,x轴上M、N两点的坐标分别为-2L和2L,则下列判断正确的是( )
电荷量不等的两点电荷固定在x轴上坐标为-3L和3L的两点,其中坐标为3L处电荷带正电,电荷量为Q.两点电荷连线上各点电势φ随x变化的关系如图所示,其中x=L处电势最低,x轴上M、N两点的坐标分别为-2L和2L,则下列判断正确的是( )
 电荷量不等的两点电荷固定在x轴上坐标为-3L和3L的两点,其中坐标为3L处电荷带正电,电荷量为Q.两点电荷连线上各点电势φ随x变化的关系如图所示,其中x=L处电势最低,x轴上M、N两点的坐标分别为-2L和2L,则下列判断正确的是( )
电荷量不等的两点电荷固定在x轴上坐标为-3L和3L的两点,其中坐标为3L处电荷带正电,电荷量为Q.两点电荷连线上各点电势φ随x变化的关系如图所示,其中x=L处电势最低,x轴上M、N两点的坐标分别为-2L和2L,则下列判断正确的是( )| A. | 两点电荷一定为异种电荷 | |
| B. | 原点O处场强大小为$\frac{kQ}{3{L}^{2}}$ | |
| C. | 负检验电荷在原点O处受到向左的电场力 | |
| D. | 负检验电荷由M点运动到N点的过程,电势能先减小后增大 |
14. 时速达到350km的郑州到西安的高速客运专线开始运营,方便了人们出行.已知郑州到西安线路全长505km,列车总长200m,动车组运行时间约2h.根据上述信息可知( )
时速达到350km的郑州到西安的高速客运专线开始运营,方便了人们出行.已知郑州到西安线路全长505km,列车总长200m,动车组运行时间约2h.根据上述信息可知( )
 时速达到350km的郑州到西安的高速客运专线开始运营,方便了人们出行.已知郑州到西安线路全长505km,列车总长200m,动车组运行时间约2h.根据上述信息可知( )
时速达到350km的郑州到西安的高速客运专线开始运营,方便了人们出行.已知郑州到西安线路全长505km,列车总长200m,动车组运行时间约2h.根据上述信息可知( )| A. | 由于动车组列车总长200 m,动车组列车在郑州到西安正常运行时不能视为质点 | |
| B. | 动车组列车在郑州到西安正常运行时的平均速率约为250 km/h | |
| C. | 动车组列车在郑州到西安正常运行时的平均速度约为350 km/h | |
| D. | 由题目信息不能求出动车组列车在郑州到西安正常运行时的平均速度 |
15.一物体从静止开始做匀加速直线运动,在第3s内通过的位移是3m,则下列说法正确的是( )
| A. | 第3 s内的平均速度是1m/s | B. | 物体的加速度是1.2 m/s2 | ||
| C. | 前3 s内的位移是6 m | D. | 3 s末的速度是4 m/s |
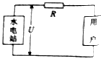 如图所示,一水电站输出的电功率P=20kW,输电电压U=400V,输电线的总电阻R=1Ω.求:
如图所示,一水电站输出的电功率P=20kW,输电电压U=400V,输电线的总电阻R=1Ω.求: