题目内容

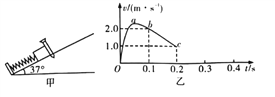
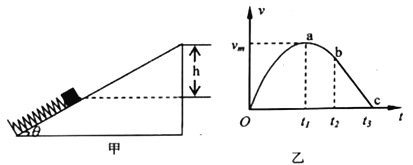
【题目】如图甲所示，下端与挡板拴接的轻弹簧置于倾角为θ=30°的斜面上，质量为m的滑块(可视为质点)用细线与挡板相连(弹簧处于压缩状态)。现剪断细线，从此时开始计时，滑块沿斜面向上运动，滑块向上运动的v-t图像如乙图所示，已知bc段是直线且滑块bc段运动的加速度大小等于重力加速度g，t=t3时滑块恰好到达斜面顶端，t=0时滑块与斜面顶点间的竖直高度为h，则下列说法正确的是

A. t1时刻弹簧恢复到自然长度，t2时刻滑块与弹簧分离

B. 滑块与斜面间的动摩擦因数为

C. 整个过程中系统损失的机械能为mgh

D. 剪断细线前弹簧具有的弹性势能为mgh

【答案】BC

【解析】t1时刻滑块的速度最大，此时加速度为零，弹簧的弹力F弹=mgsinθ+μmgcosθ，此时弹簧仍处于压缩状态；t2时刻滑块开始做匀减速运动，此时与弹簧分离，选项A错误；对滑块从t2到t3时间内，由牛顿第二定律： ，解得，选项B正确；整个过程中系统损失的机械能等于客服摩擦力做功，即，选项C正确；剪断细线前弹簧具有的弹性势能等于重力势能的增量与摩擦力做功之和，即2mgh，选项D错误；故选BC.

练习册系列答案
相关题目

【题目】如图为振幅、频率相同的两列横波在t=0时刻相遇时形成的干涉图样，实线与虚线分别表示波峰和波谷，已知两列波的振幅均为5cm，波速和波长均为1m/s和0.4m。下列说法正确的是_________。（填正确答案标号。选对1个得2分，选对2个得4分，选对3个得5分。每选错1个扣3分，最低得分0分）。

A.P点始终处于波谷位置

B.R、S两点始终处于静止状态

C.Q点在t=0.1s时刻将处于平衡位置

D.从t=0到t=0.2s的时间内，Q点通过的路程为20cm

E.如果A、B两波源频率不同，也能产生类似的稳定的干涉现象

【答案】BCD

【解析】A、此时P点波谷与波谷相遇，振动加强点，但不是总是处于波谷位置，不过总是处于振动加强点，故A错误；

B、R、S两点是波峰与波谷相遇，振动减弱，位移为零，始终处于静止状态，故B正确；

C、Q是波峰与波峰相遇，所以Q点在图中所示的时刻处于波峰，再过周期处于平衡位置，故C正确；

D、Q是波峰与波峰相遇，从t=0到t=0.2s的时间内， Q点通过的路程为，故D正确；

E、两列波相遇发生干涉的必要条件是：两列波的频率相同，故E错误；故选BCD。

【题型】填空题
【结束】
16

【题目】如图所示，有一透明的柱形元件，其横截面是半径为R的圆弧，圆心为O，以O为原点建立直角坐标系xOy。一束单色光平行于x轴射入该元件，入射点的坐标为，单色光对此元件的折射率为，不考虑单色光经圆弧面反射后的情况。

①当d多大时，该单色光在圆弧面上刚好发生全反射？

②当时，求该单色光照射到x轴上的位置到圆心O的距离。（很小时， ）

【题目】如图甲所示，在倾角为37°足够长的粗糙斜面底端，一轻弹簧被一质量m=1kg的滑块(可视为质点)压缩着且位置锁定，但它们并不粘连。t=0时解除锁定，计算机通过传感器描绘出滑块的v—t图象如图乙所示，其中Oab段为曲线，bc段为直线，在t1=0.1s时滑块已上滑s=0.25m的距离(g取10m/s2，sin37°=0.6，cos37°=0.8)。则下列说法正确的是（ ）

A. 滑块与斜面之间的动摩擦因数μ=0.2

B. 弹簧锁定时具有的弹性势能EP=4.5J

C. 当t=0.3s时滑块的速度大小为0

D. 当t=0.4s时滑块的速度大小为1m/s

【题目】如图所示，一绝热气缸竖直放置，一定质量的理想气体被活塞封闭于气缸中，绝热活塞质量为m、横截面积为S，不计厚度，且与气缸壁之间没有摩擦。开始时活塞被销子K固定于距气缸底部高度为h1的A位置，气体温度为T1，压强为p1，现拔掉销子，活塞下降到距气缸底部高度为h2的B位置时停下，已知大气压强为p0，重力加速度为g。

（i）求此时气体温度TB；

（ii）若再用电热丝给气体缓慢加热，使活塞上升到距气缸底部高度为h3的C位置时停下，求活塞上升过程中气体对活塞做的功。

【题目】如图所示为雨滴从高空下落过程中空气阻力f随雨滴速度v变化的大致情况，其中图线①、②分别对应半径不同的雨滴。

（1）请利用图线分析并说明雨滴下落过程中加速度和速度随时间变化的大致情况。

（2）已知图中直线的斜率值，其中 kg/（m2· s），r为雨滴的半径。（雨滴的密度取ρ=1.0×103kg/m3）请比较①、②图线所示的两个雨滴下落的最终速度；请计算半径r=5mm的雨滴下落的最终速度。

【题目】两平行且电阻不计的金属导轨相距L=1m，金属导轨由水平和倾斜两部分(均足够长)良好对接，倾斜部分与水平方向的夹角为37°，整个装置处在竖直向上、磁感应强度B=2T的匀强磁场中。长度也为1m的金属棒ab和cd垂直导轨跨搁，且与导轨良好接触，质量均为0.2kg，电阻分别为R1=2Ω，R2=4Ω。ab置于导轨的水平部分，与导轨的动摩擦因数为μ=0.5，cd置于导轨的倾斜部分，导轨倾斜部分光滑。从t=0时刻起，ab棒在水平且垂直于ab棒的外力F1的作用下由静止开始向右做匀加速直线运动，金属棒cd在力F2的作用下保持静止，F2平行于倾斜导轨平面且垂直于金属杆cd。当t1=4s时， ab棒消耗的电功率为2.88W。已知sin37°=0.6， cos37°=0.8，重力加速度g=10m/s2。求：

(1)ab棒做匀加速直线运动的加速度大小；

(2)求t2=8s时作用在cd棒上的F2；

(3)改变F1的作用规律，使ab棒运动的位移x与速度v。满足：x=2v，要求cd仍然要保持静止状态。求ab棒从静止开始运动x=4m的过程中，作用在ab棒上的力F1所做的功(结果可用分数表示).

【题目】如图所示，边长为L的等边三角形ABC的三个顶点上分别固定一个点电荷，所带电荷量依次为+q、+q和－q。D点和M点分别为AB边和AC边的中点，N点为三角形的中心，静电力常量为k。在该电场中，下列说法正确的是 ( )

A. D点的电场强度大小为，方向为从N指向D

B. N点的电场强度大小为，方向为从N指向C

C. D点的电势高于N点的电势

D. 若取无穷远处电势为0，则M点的电势为0

【题目】如图甲所示是研究小车加速度与力关系的实验装置，木板置于水平桌面上，一端系有 沙桶的细绳通过滑轮与拉力传感器相连，拉力传感器可显示所受的拉力大小F，改变桶中砂的质量多次实验。完成下列问题：

（1）实验中需要_____。

A．测量砂和砂桶的总质量

B．保持细线与长木板平行

C．保持小车的质量不变

D．满足砂和砂桶的总质量远小于小车的质量

（2）实验中得到一条纸带，相邻计数点间有四个点未标出，各计数点到A点的距离如图乙所示。电源的频率为50HZ，则打B点时小车速度大小为_____m/s，小车的加速度大小为_____m/s2。

（3）实验中描绘出a-F图象如图丙所示，图象不过坐标原点的原因是______________________________。

【题目】某实验小组想在实验室测量一电源的电动势及内阻，但内阻为2k9的电压表量程3V不够，现需改装电压表后再进行实验。

(1)改装成量程为9V的电压表需串联R0=____________kΩ的电阻；

(2)利用一个电阻箱R(符号)、一只开关S、若干导线和改装后的电压表(用原来电压表的符号和串联电阻R0表示，且此电压表可视为理想电表)测量电源电动势及内阻，请画出的实验电路图_____；

(3)根据以上实验电路图进行实验时，如果读出电压表示数为1.50V时，电阻箱的阻值为15.0Ω，则电源的电动势E和内阻r的关系式为E=____________。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网