题目内容
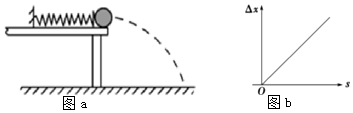
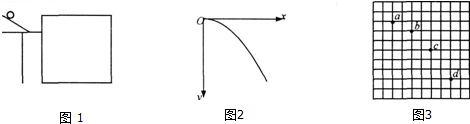
1.如图1所示是研究平抛运动的实验装置简图,图2是实验后白纸上的轨迹图.(1)说明图中的两条坐标轴是如何作出的利用重锤线作出Oy轴,过O点作Oy轴的垂线为Ox轴
(2)坐标原点O的准确位置应该在球心处
(3)用一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm,若小球在平抛运动途中的几个位置如图3中a、b、c、d所示,则小球平抛的初速度为v0=2$\sqrt{gL}$(用L、g表示),其值是0.7m/s.(g取9.8m/s2)
分析 根据竖直方向上相等时间内的位移之差是一恒量求出相等时间间隔,结合水平位移和时间间隔求出初速度的表达式.
解答 解:(1)利用重锤线作出Oy轴,过O点作Oy轴的垂线为Ox轴.如图所示: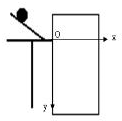
(2)坐标原点O的准确位置应该在球心处.
(3)竖直方向上有:△y=L=gT2,
解得:T=$\sqrt{\frac{L}{g}}$,
则初速度为:v0=$\frac{2L}{T}$=2L$\sqrt{\frac{g}{L}}$=2$\sqrt{gL}$.
代入数据得:v0=2$\sqrt{10×0.0125}$=0.7m/s.
故答案为:(1)利用重锤线作出Oy轴,过O点作Oy轴的垂线为Ox轴;(2)球心处;(3)2$\sqrt{gL}$,0.7m/s.
点评 解决本题的关键知道平抛运动在水平方向做匀速直线运动,竖直方向上做自由落体运动,结合运动学公式和推论灵活求解.

练习册系列答案
相关题目
11.简谐机械波在给定的媒质中传播时,下列说法正确的是( )
| A. | 振幅越大,则波传播的速度越快 | |
| B. | 振幅越大,则波传播的速度越慢 | |
| C. | 在一个周期内,振动质元走过的路程等于一个波长 | |
| D. | 振动的频率越高,则波传播一个波长的距离所用的时间越短 |
9.欲使处于基态的氢原子发生电离,下列措施可行的是( )
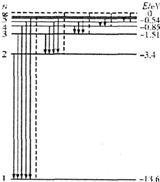

| A. | 用10.2 eV的光子照射 | B. | 用11eV的光子照射 | ||
| C. | 用14 eV的光子照射 | D. | 用10eV的电子碰撞 |
16.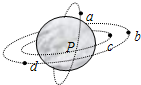 如图所示,a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d在同一个圆轨道上.某时刻b卫星恰好处于C卫星的正上方.下列说法中正确的是( )
如图所示,a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d在同一个圆轨道上.某时刻b卫星恰好处于C卫星的正上方.下列说法中正确的是( )
 如图所示,a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d在同一个圆轨道上.某时刻b卫星恰好处于C卫星的正上方.下列说法中正确的是( )
如图所示,a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d在同一个圆轨道上.某时刻b卫星恰好处于C卫星的正上方.下列说法中正确的是( )| A. | a、c的线速度大小相等,且小于d的线速度 | |
| B. | a、c的加速度大小相等,且大于b的加速度 | |
| C. | a、c的向心力大小相等 | |
| D. | b、C的角速度大小相等,且小于a的角速度 |
13.质量为m的物体(可视为质点)沿着倾角为θ的光滑斜面由顶端开始下滑,当物体滑至斜面底端时瞬时速率v,此时重力的瞬时功率为( )
| A. | mgv | B. | mgvsinθ | C. | mgvcosθ | D. | mgvtanθ |
10.某交流发电机产生的感应电动势与时间的关系如图所示.由图象可知( )
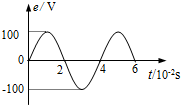

| A. | 交流电的周期为0.06s | B. | 交流电的频率为50Hz | ||
| C. | 线圈转动的角速度为50rad/s | D. | 电动势的瞬时值为e=100sin50πt(V) |
11.用比值法定义物理量是物理学中一种很重要的思想方法,下列表达中不属于比值法定义物理量的是( )
| A. | 电势差UAB=$\frac{{{W_{AB}}}}{q}$ | B. | 电容C=$\frac{Q}{U}$ | C. | 电场强度E=$\frac{F}{q}$ | D. | 电容C=$\frac{εs}{4πkd}$ |
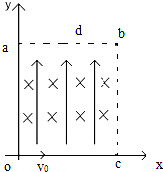 如图所示,在竖直平面内的直角坐标系xoy中,有正方形区域oabc,其区域内存在竖直向上大小为的E匀强电场.不加磁场时,一带电小球以初速度V0从o点沿X轴正方向射入,恰好沿X轴做匀速直线运动.若加一垂直于平面向里、大小为B的匀强磁场,小球恰好能在oabc区域内做匀速圆周运动,从a点沿x轴负方向射出该区域,已知重力加速度为g,求:
如图所示,在竖直平面内的直角坐标系xoy中,有正方形区域oabc,其区域内存在竖直向上大小为的E匀强电场.不加磁场时,一带电小球以初速度V0从o点沿X轴正方向射入,恰好沿X轴做匀速直线运动.若加一垂直于平面向里、大小为B的匀强磁场,小球恰好能在oabc区域内做匀速圆周运动,从a点沿x轴负方向射出该区域,已知重力加速度为g,求: