题目内容
12. 如图所示,在竖直平面内的直角坐标系xoy中,有正方形区域oabc,其区域内存在竖直向上大小为的E匀强电场.不加磁场时,一带电小球以初速度V0从o点沿X轴正方向射入,恰好沿X轴做匀速直线运动.若加一垂直于平面向里、大小为B的匀强磁场,小球恰好能在oabc区域内做匀速圆周运动,从a点沿x轴负方向射出该区域,已知重力加速度为g,求:
如图所示,在竖直平面内的直角坐标系xoy中,有正方形区域oabc,其区域内存在竖直向上大小为的E匀强电场.不加磁场时,一带电小球以初速度V0从o点沿X轴正方向射入,恰好沿X轴做匀速直线运动.若加一垂直于平面向里、大小为B的匀强磁场,小球恰好能在oabc区域内做匀速圆周运动,从a点沿x轴负方向射出该区域,已知重力加速度为g,求:(1)带电小球电性及比荷$\frac{q}{m}$;
(2)若同时存在电场和磁场,带小球从o点入射的同时,磁场的上边界以某一速度V向下匀速运动,使得带电体刚好从ab边上的中点d飞出电场,求V.
分析 (1)根据平衡条件,判定电性,再由平衡方程,从而求得比荷;
(2)根据牛顿第二定律,结合向心力表达式与运动学公式,及周期公式,即可求解.
解答 解:(1)、由平衡条件可知,物体带正电,
则有:mg=qE
解得:$\frac{q}{m}$=$\frac{g}{E}$
(2)、根据牛顿第二定律,由洛伦兹力提供向心力,则为:qv0B=m$\frac{{v}_{0}^{2}}{R}$,
解得:R=$\frac{{E{V_0}}}{gB}$
因V•t=R
由t=$\frac{θ}{2π}•T$=$\frac{T}{4}$
且T=$\frac{2πm}{qB}$
联立上式,解得:V=$\frac{2{v}_{0}}{π}$
答:(1)小球带正电及比荷$\frac{g}{E}$;
(2)若同时存在电场和磁场,带小球从o点入射的同时,磁场的上边界以某一速度V向下匀速运动,使得带电体刚好从ab边上的中点d飞出电场,则速度为$\frac{2{v}_{0}}{π}$.
点评 考查平衡条件与牛顿第二定律的应用,掌握圆周运动的半径与周期公式的内容,理解向心力表达式.

练习册系列答案
相关题目
2. 小船横渡一条两岸平行的河流,船本身提供的速度(即船的静水速度)大小不变、船身方向始终垂直于河岸,水流速度与河岸平行,已知小船的运动轨迹如图所示,则下列说法正确的是( )
小船横渡一条两岸平行的河流,船本身提供的速度(即船的静水速度)大小不变、船身方向始终垂直于河岸,水流速度与河岸平行,已知小船的运动轨迹如图所示,则下列说法正确的是( )
 小船横渡一条两岸平行的河流,船本身提供的速度(即船的静水速度)大小不变、船身方向始终垂直于河岸,水流速度与河岸平行,已知小船的运动轨迹如图所示,则下列说法正确的是( )
小船横渡一条两岸平行的河流,船本身提供的速度(即船的静水速度)大小不变、船身方向始终垂直于河岸,水流速度与河岸平行,已知小船的运动轨迹如图所示,则下列说法正确的是( )| A. | 越接近河岸水流速度越大 | |
| B. | 各处水流速度大小一样 | |
| C. | 无论水流速度是否变化,这种渡河方式时间一定最短 | |
| D. | 该船渡河的时间会受水流速度变化的影响 |
7. “研究电磁感应现象”的实验采用了如图所示的装置,当滑动变阻器R的滑片P不动时,甲、乙两个相同的电流表的指针位置如图所示,当滑片P较快地向a端滑动时,两表指针的偏转方向是( )
“研究电磁感应现象”的实验采用了如图所示的装置,当滑动变阻器R的滑片P不动时,甲、乙两个相同的电流表的指针位置如图所示,当滑片P较快地向a端滑动时,两表指针的偏转方向是( )
 “研究电磁感应现象”的实验采用了如图所示的装置,当滑动变阻器R的滑片P不动时,甲、乙两个相同的电流表的指针位置如图所示,当滑片P较快地向a端滑动时,两表指针的偏转方向是( )
“研究电磁感应现象”的实验采用了如图所示的装置,当滑动变阻器R的滑片P不动时,甲、乙两个相同的电流表的指针位置如图所示,当滑片P较快地向a端滑动时,两表指针的偏转方向是( )| A. | 甲、乙两表指针都向左偏 | B. | 甲、乙两表指针都向右偏 | ||
| C. | 甲表指针向左偏,乙表指针向右偏 | D. | 甲表指针向右偏,乙表指针向左偏 |
17.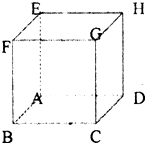 如图所示,在真空中的正方体(边长为l)的七个顶点上分别同定+Q的点电荷,在另外的一个顶点上同定-Q的点电荷,则这八个点电荷在正方体的中心处产生的合场强为(k为静电力常量)( )
如图所示,在真空中的正方体(边长为l)的七个顶点上分别同定+Q的点电荷,在另外的一个顶点上同定-Q的点电荷,则这八个点电荷在正方体的中心处产生的合场强为(k为静电力常量)( )
 如图所示,在真空中的正方体(边长为l)的七个顶点上分别同定+Q的点电荷,在另外的一个顶点上同定-Q的点电荷,则这八个点电荷在正方体的中心处产生的合场强为(k为静电力常量)( )
如图所示,在真空中的正方体(边长为l)的七个顶点上分别同定+Q的点电荷,在另外的一个顶点上同定-Q的点电荷,则这八个点电荷在正方体的中心处产生的合场强为(k为静电力常量)( )| A. | 0 | B. | $\frac{8kQ}{3{l}^{2}}$ | C. | $\frac{4kQ}{3{l}^{2}}$ | D. | $\frac{4kQ}{{l}^{2}}$ |
 如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的 两端,当A物体以速度v向左运动时,系A、B的绳分别与水平方向成α、β角,此时B物体的速度大小为$\frac{cosα}{cosβ}$v,方向水平向右.
如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的 两端,当A物体以速度v向左运动时,系A、B的绳分别与水平方向成α、β角,此时B物体的速度大小为$\frac{cosα}{cosβ}$v,方向水平向右. “验证机械能守恒定律”的实验中
“验证机械能守恒定律”的实验中
