题目内容
 如图,在光滑的水平面上,停着一辆平板小车,小车的质量为M=10kg.在小车左端A处,放有质量为m=5kg的小物体(可视为质点),现给小物体一个I=30N?S的瞬时冲量,物体在平板车上相对于小车向右滑行L=1.5m后被弹回,最后刚好在A点与车保持相对静止.求:
如图,在光滑的水平面上,停着一辆平板小车,小车的质量为M=10kg.在小车左端A处,放有质量为m=5kg的小物体(可视为质点),现给小物体一个I=30N?S的瞬时冲量,物体在平板车上相对于小车向右滑行L=1.5m后被弹回,最后刚好在A点与车保持相对静止.求:(1)物体与平板车间的动摩擦因数μ.
(2)弹簧在压缩过程中所具有的最大弹性势能EP.
分析:(1)给小物体一个I=30N?S的瞬时冲量,先根据动量定理求出物体获得的速度.物体在小车运动的过程中,系统的动量守恒,当两者相对静止时速度相同,由动量守恒定律求出共同速度,由能量守恒列式,即可求得μ.
(2)弹簧压缩量最大时弹性势能最大,此时物体与小车的速度相同,由动量守恒可求得此时的共同速度,对于物体在小车开始运动到弹簧压缩到最短的过程,运用能量守恒列式,即可求得弹簧最大弹性势能EP.
(2)弹簧压缩量最大时弹性势能最大,此时物体与小车的速度相同,由动量守恒可求得此时的共同速度,对于物体在小车开始运动到弹簧压缩到最短的过程,运用能量守恒列式,即可求得弹簧最大弹性势能EP.
解答:解:(1)对物体,由动量定理得 I=mv0
解得:v0=
=6m/s
对于物体、小车及弹簧组成的系统,全过程动量守恒,设物体刚好回到A点时的速度为v,则有
mv0=(m+M)v,得v=
=2m/s
又由能量守恒得:
m
=
(m+M)v2+μmg?2L
代入数据解得,μ=0.4
(2)当弹簧具有最大弹性势能时物体与小车的速度相等,也是v,同样由能量守恒得
m
=
(M+m)v2+μmgL+Ep
解得:Ep=30J
答:
(1)物体与平板车间的动摩擦因数μ是0.4.
(2)弹簧在压缩过程中所具有的最大弹性势能EP是30J.
解得:v0=
| I |
| m |
对于物体、小车及弹簧组成的系统,全过程动量守恒,设物体刚好回到A点时的速度为v,则有
mv0=(m+M)v,得v=
| mv0 |
| m+M |
又由能量守恒得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
代入数据解得,μ=0.4
(2)当弹簧具有最大弹性势能时物体与小车的速度相等,也是v,同样由能量守恒得
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
解得:Ep=30J
答:
(1)物体与平板车间的动摩擦因数μ是0.4.
(2)弹簧在压缩过程中所具有的最大弹性势能EP是30J.
点评:整个运动的过程中,系统的动量守恒,针对不同的过程,根据动量守恒和能量守恒计算即可.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
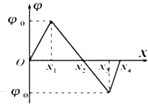 在光滑的水平面内有一沿x轴的静电场,其电势φ随x坐标值的变化图线如图所示.一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动.下列叙述正确的是( )
在光滑的水平面内有一沿x轴的静电场,其电势φ随x坐标值的变化图线如图所示.一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动.下列叙述正确的是( )| A、若小球能运动到x1处,则该过程小球所受电场力逐渐增大 | ||||||||
| B、带电小球从x1运动到x3的过程中,电势能先减小后增大 | ||||||||
C、若该小球能运动到x4处,则初速度v0至少为2
| ||||||||
D、若v0为2
|
 在光滑的水平面内,一质量m=1kg的质点以速度V0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=15N作用,直线OA与x轴成a=37°,如图所示曲线为质点的轨迹图(g取10m/s2 sin37°=0.6 cos37°=0.8 ) 求:
在光滑的水平面内,一质量m=1kg的质点以速度V0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=15N作用,直线OA与x轴成a=37°,如图所示曲线为质点的轨迹图(g取10m/s2 sin37°=0.6 cos37°=0.8 ) 求: 如图,在光滑水平面内的弹簧振子连接一根长软绳,以平衡位置O点为原点沿绳方向取x轴.振子从O以某一初速度向A端开始运动,振动频率为f=10Hz,当振子从O点出发后,第二次返回O点时,软绳上x=15cm处的质点恰好第一次到达波峰,则下列说法正确的是( )
如图,在光滑水平面内的弹簧振子连接一根长软绳,以平衡位置O点为原点沿绳方向取x轴.振子从O以某一初速度向A端开始运动,振动频率为f=10Hz,当振子从O点出发后,第二次返回O点时,软绳上x=15cm处的质点恰好第一次到达波峰,则下列说法正确的是( )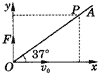 在光滑的水平面内,一质量m=1kg的质点,以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=5N作用,直线OA与x轴成37°角,如图所示.如果质点的运动轨迹与直线OA相交于P点,则质点从O点到P点所经历的时间为
在光滑的水平面内,一质量m=1kg的质点,以速度v0=10m/s沿x轴正方向运动,经过原点后受一沿y轴正方向的恒力F=5N作用,直线OA与x轴成37°角,如图所示.如果质点的运动轨迹与直线OA相交于P点,则质点从O点到P点所经历的时间为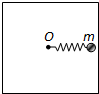 如图所示,在光滑的水平面内,用轻弹簧拉住一质量为m的小球,轻弹簧的另一端固定在转轴上的O点.轻弹簧的劲度系数为k,原长为l.求小球绕O点转动的角速度分别为ω1=
如图所示,在光滑的水平面内,用轻弹簧拉住一质量为m的小球,轻弹簧的另一端固定在转轴上的O点.轻弹簧的劲度系数为k,原长为l.求小球绕O点转动的角速度分别为ω1=