题目内容
11. 如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为53°的光滑斜面上.一长为L=9cm的轻质细绳一端固定在O点,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球在位置C由静止释放,小球到达最低点D时,细绳刚好被拉断.之后小球在运动过程中恰好沿斜面方向将弹簧压缩,最大压缩量为x=5cm.(g=10m/s2,sin 53°=0.8,cos 53°=0.6)求:
如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为53°的光滑斜面上.一长为L=9cm的轻质细绳一端固定在O点,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球在位置C由静止释放,小球到达最低点D时,细绳刚好被拉断.之后小球在运动过程中恰好沿斜面方向将弹簧压缩,最大压缩量为x=5cm.(g=10m/s2,sin 53°=0.8,cos 53°=0.6)求:(1)细绳受到的拉力的最大值;
(2)D点到水平线AB的高度h;
(3)弹簧所获得的最大弹性势能Ep.
分析 (1)根据机械能守恒定律求出小球在D点的速度,再根据竖直方向上的合力提供向心力,运用牛顿第二定律求出绳子的最大拉力.
(2)球在运动过程中恰好沿斜面方向将弹簧压缩,知绳子断裂后,做平抛运动,由平抛运动的规律求h.
(3)根据速度的合成求出A点的速度,根据系统机械能守恒求出弹簧的最大弹性势能.
解答 解:(1)小球由C到D,由机械能守恒定律得:mgL=$\frac{1}{2}$m${v}_{1}^{2}$
解得:v1=$\sqrt{2gL}$…①
在D点,由牛顿第二定律得:F-mg=m$\frac{{v}_{1}^{2}}{L}$…②
由①②解得:F=30 N
由牛顿第三定律知细绳所能承受的最大拉力为 30 N.
(2)由D到A,小球做平抛运动,则得 vy2=2gh…③
由 tan53°=$\frac{{v}_{y}}{{v}_{1}}$…④
联立解得h=0.16m
(3)小球从C点到将弹簧压缩至最短的过程中,小球与弹簧系统的机械能守恒,即:
Ep=mg(L+h+xsin 53°)
代入数据得:Ep=2.9 J.
答:(1)细绳受到的拉力的最大值为30 N.
(2)D点到水平线AB的高度h为0.16m.
(3)弹簧所获得的最大弹性势能Ep为2.9 J
点评 本题考查了圆周运动、平抛运动等知识点,综合运用了牛顿第二定律、机械能守恒定律,关键是理清运动过程,选择合适的规律进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图所示,一质量为M的木块与水平面接触,木块上方固定有一根直立的绝缘轻弹簧,弹上端系一带电且质量为m的小球(弹簧不带电),小球在竖直方向上振动,当加上竖直方向的匀强电场后,在弹簧正好恢复到原长时,小球具有最大速度.当木块对水平面压力为零时,小球的加速度大小是( )
如图所示,一质量为M的木块与水平面接触,木块上方固定有一根直立的绝缘轻弹簧,弹上端系一带电且质量为m的小球(弹簧不带电),小球在竖直方向上振动,当加上竖直方向的匀强电场后,在弹簧正好恢复到原长时,小球具有最大速度.当木块对水平面压力为零时,小球的加速度大小是( )
 如图所示,一质量为M的木块与水平面接触,木块上方固定有一根直立的绝缘轻弹簧,弹上端系一带电且质量为m的小球(弹簧不带电),小球在竖直方向上振动,当加上竖直方向的匀强电场后,在弹簧正好恢复到原长时,小球具有最大速度.当木块对水平面压力为零时,小球的加速度大小是( )
如图所示,一质量为M的木块与水平面接触,木块上方固定有一根直立的绝缘轻弹簧,弹上端系一带电且质量为m的小球(弹簧不带电),小球在竖直方向上振动,当加上竖直方向的匀强电场后,在弹簧正好恢复到原长时,小球具有最大速度.当木块对水平面压力为零时,小球的加速度大小是( )| A. | $\frac{mg}{M}$ | B. | $\frac{(M+m)g}{m}$ | C. | $\frac{Mg}{m}$ | D. | $\frac{(M+m)g}{M}$ |
2.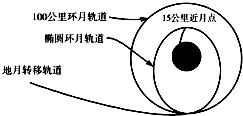 2013年12月2日,“长征三号乙”运载火箭将“嫦娥三号”月球探测器成功送入太空,12月6日“嫦娥三号”由地月转移轨道进入100公里环月轨道,12月10日成功变轨到近月点为15公里的椭圆轨道,12月14日从15公里高度降至月球表面成功实现登月.则关于“嫦娥三号”登月过程的说法正确的是( )
2013年12月2日,“长征三号乙”运载火箭将“嫦娥三号”月球探测器成功送入太空,12月6日“嫦娥三号”由地月转移轨道进入100公里环月轨道,12月10日成功变轨到近月点为15公里的椭圆轨道,12月14日从15公里高度降至月球表面成功实现登月.则关于“嫦娥三号”登月过程的说法正确的是( )
 2013年12月2日,“长征三号乙”运载火箭将“嫦娥三号”月球探测器成功送入太空,12月6日“嫦娥三号”由地月转移轨道进入100公里环月轨道,12月10日成功变轨到近月点为15公里的椭圆轨道,12月14日从15公里高度降至月球表面成功实现登月.则关于“嫦娥三号”登月过程的说法正确的是( )
2013年12月2日,“长征三号乙”运载火箭将“嫦娥三号”月球探测器成功送入太空,12月6日“嫦娥三号”由地月转移轨道进入100公里环月轨道,12月10日成功变轨到近月点为15公里的椭圆轨道,12月14日从15公里高度降至月球表面成功实现登月.则关于“嫦娥三号”登月过程的说法正确的是( )| A. | “嫦娥三号”由地月转移轨道需要减速才能进入100公里环月轨道 | |
| B. | “嫦娥三号”在近月点为15公里的椭圆轨道上各点的速度都大于其在100公里圆轨道上的速度 | |
| C. | “嫦娥三号”在100公里圆轨道上运动的周期小于其在近月点为15公里的椭圆轨道上运动的周期 | |
| D. | 从15公里高度降至月球表面过程中,“嫦娥三号”处于失重状态 |
19.用容积为V1的活塞式抽气机给容积为V2的密闭牛顿管抽气,若抽气过程中气体温度不变,则抽气两次后,牛顿管中剩余气体中的压强是原来的.( )
| A. | ($\frac{{v}_{2}}{{v}_{1}+{v}_{2}}$)2 | B. | ($\frac{{v}_{1}}{{v}_{1}+{v}_{2}}$)2 | C. | $\frac{{v}_{1}}{2{v}_{1}+{v}_{2}}$ | D. | $\frac{{v}_{1}}{{v}_{1}+2{v}_{2}}$ |
16.下列说法正确的是 ( )
| A. | 为了保存玉米地的水分,可以锄松地面,破坏土壤里的毛细管 | |
| B. | 利用浅层海水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的 | |
| C. | 外界对物体做功,物体的内能必定增加 | |
| D. | 液晶的光学性质不随温度、电磁作用变化而改变 | |
| E. | 物质是晶体还是非晶体,比较可靠的办法是从熔化过程温度是否变化来判断. |
20. 如图所示,竖直平面内有平行放置的光滑导轨,导轨间距为L,电阻不计,导轨间有水平方向的匀强磁场,磁感应强度大小为B=2T,方向如图所示.有两根质量均为m=0.1kg、长度均为L=0.2m、电阻均为R=0.4Ω的导体棒ab和cd与导轨接触良好,当用竖直向上的力F使ab棒向上做匀速运动时,cd棒刚好能静止不动,则下列说法正确的是(g取10m/s2)( )
如图所示,竖直平面内有平行放置的光滑导轨,导轨间距为L,电阻不计,导轨间有水平方向的匀强磁场,磁感应强度大小为B=2T,方向如图所示.有两根质量均为m=0.1kg、长度均为L=0.2m、电阻均为R=0.4Ω的导体棒ab和cd与导轨接触良好,当用竖直向上的力F使ab棒向上做匀速运动时,cd棒刚好能静止不动,则下列说法正确的是(g取10m/s2)( )
 如图所示,竖直平面内有平行放置的光滑导轨,导轨间距为L,电阻不计,导轨间有水平方向的匀强磁场,磁感应强度大小为B=2T,方向如图所示.有两根质量均为m=0.1kg、长度均为L=0.2m、电阻均为R=0.4Ω的导体棒ab和cd与导轨接触良好,当用竖直向上的力F使ab棒向上做匀速运动时,cd棒刚好能静止不动,则下列说法正确的是(g取10m/s2)( )
如图所示,竖直平面内有平行放置的光滑导轨,导轨间距为L,电阻不计,导轨间有水平方向的匀强磁场,磁感应强度大小为B=2T,方向如图所示.有两根质量均为m=0.1kg、长度均为L=0.2m、电阻均为R=0.4Ω的导体棒ab和cd与导轨接触良好,当用竖直向上的力F使ab棒向上做匀速运动时,cd棒刚好能静止不动,则下列说法正确的是(g取10m/s2)( )| A. | ab棒的运动速度是5m/s | B. | 力F的大小为1N | ||
| C. | 在1s内,力F做的功为5 J | D. | 在1s内,cd棒产生的电热为2.5J |
1. 如图所示,固定在水平面上的光滑平行金属导轨,间距为L,右端接有阻值为R的电阻,空间存在方向竖直、磁感应强度为B的匀强磁场.质量为m、电阻为r的导体棒ab与固定弹簧相连,放在导轨上.初始时刻,弹簧恰处于自然长度.给导体棒水平向右的初速度v0,导体棒开始沿导轨往复运动,最终停在初始位置.在此过程中,导体棒始终与导轨垂直并保持良好接触.已知导体棒的电阻r与定值电阻R的阻值相等,不计导轨电阻,则下列说法中正确的是( )
如图所示,固定在水平面上的光滑平行金属导轨,间距为L,右端接有阻值为R的电阻,空间存在方向竖直、磁感应强度为B的匀强磁场.质量为m、电阻为r的导体棒ab与固定弹簧相连,放在导轨上.初始时刻,弹簧恰处于自然长度.给导体棒水平向右的初速度v0,导体棒开始沿导轨往复运动,最终停在初始位置.在此过程中,导体棒始终与导轨垂直并保持良好接触.已知导体棒的电阻r与定值电阻R的阻值相等,不计导轨电阻,则下列说法中正确的是( )
 如图所示,固定在水平面上的光滑平行金属导轨,间距为L,右端接有阻值为R的电阻,空间存在方向竖直、磁感应强度为B的匀强磁场.质量为m、电阻为r的导体棒ab与固定弹簧相连,放在导轨上.初始时刻,弹簧恰处于自然长度.给导体棒水平向右的初速度v0,导体棒开始沿导轨往复运动,最终停在初始位置.在此过程中,导体棒始终与导轨垂直并保持良好接触.已知导体棒的电阻r与定值电阻R的阻值相等,不计导轨电阻,则下列说法中正确的是( )
如图所示,固定在水平面上的光滑平行金属导轨,间距为L,右端接有阻值为R的电阻,空间存在方向竖直、磁感应强度为B的匀强磁场.质量为m、电阻为r的导体棒ab与固定弹簧相连,放在导轨上.初始时刻,弹簧恰处于自然长度.给导体棒水平向右的初速度v0,导体棒开始沿导轨往复运动,最终停在初始位置.在此过程中,导体棒始终与导轨垂直并保持良好接触.已知导体棒的电阻r与定值电阻R的阻值相等,不计导轨电阻,则下列说法中正确的是( )| A. | 导体棒开始运动的初始时刻受到的安培力向左 | |
| B. | 导体棒开始运动的初始时刻导体棒两端的电压U=BLv0 | |
| C. | 导体棒开始运动后速度第一次为零时,系统的弹性势能Ep=$\frac{1}{2}$mv02 | |
| D. | 在金属棒整个运动过程中,电阻R上产生的焦耳热Q=$\frac{1}{4}$mv02 |
