题目内容
6.某同学利用如图甲所示的实验装置运用牛顿第二定律测量滑块的质量M.主要步骤为:
(1)调整长木板倾角,当钩码的质量为m0时滑块沿木板恰好向下做匀速运动.
(2)保持木板倾角不变,撤去钩码m0,将滑块移近打点计时器,然后释放滑块,滑块沿木板向下做匀加速直线运动,并打出点迹清晰的纸带如图乙所示(已知打点计时器每隔0.02s打下一个点).
请回答下列问题:
(Ⅰ)打点计时器在打下B点时滑块的速度υB=1.38m/s;
(Ⅱ)滑块做匀加速直线运动的加速度a=3.88m/s2;
(Ⅲ)滑块质量M=$\frac{{m}_{0}g}{a}$(用字母a、m0、当地重力加速度g表示).
(3)保持木板倾角不变,挂上质量为m(均小于m0)的钩码,滑块沿木板向下匀加速运动,测出滑块的加速度;多次改变钩码的质量,分别求出相应的加速度.
(4)若绳的拉力与所挂钩码的重力大小相等,作出的a-mg图象如图丙所示,则由图丙可求得滑块的质量M=0.200kg.(取g=10m/s2,计算结果均保留3位有效数字)
分析 根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小;
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小;
当取下细绳和钩码时,由于滑块所受其它力不变,因此其合外力与撤掉钩码的重力等大反向;
根据牛顿第二定律有mg=Ma,由此可解得滑块的质量.
解答 解:(2)由图示纸带可知,两个相邻两个计数点间还有1个点没有画出,所以相邻的计数点间的时间间隔t=2T=0.04s,
(Ⅰ)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上B点时小车的瞬时速度大小.
vC=$\frac{{x}_{AC}}{2t}$=$\frac{0.0520+0.0584}{2×0.04}$=1.38m/s;
(Ⅱ)根据匀变速直线运动的推论公式△x=at2可以知,加速度的大小:
a=$\frac{{x}_{CD}-{x}_{AB}+{x}_{DE}-{x}_{BC}}{4{T}^{2}}$=$\frac{0.0645-0.0520+0.0707-0.0584}{4×0.0{4}^{2}}$=3.88m/s2.
(Ⅲ)滑块做匀速运动时受力平衡作用,由平衡条件得:m0g=Mgsinθ-f,撤去m0时滑块做匀加速直线运动时,受到的合外力:F合=Mgsinθ-f,由牛顿第二定律得:F合=Ma,解得:M=$\frac{{m}_{0}g}{a}$.
(4)滑块做匀速运动时受力平衡作用,由平衡条件得:Mgsinθ-f=0,挂上质量为m的钩码时滑块沿木板向下做匀加速直线运动,受到的合外力为:F合′=Mgsinθ-f-mg,由牛顿第二定律得:F合′=Ma,解得:a=-$\frac{m}{M}$g,由图丙所示图象可知:k=$\frac{1}{M}$=$\frac{3.5-2.5}{0.20}$=5,解得:M=0.200kg.
故答案为:(2)(Ⅰ)1.38;(Ⅱ)3.88;(Ⅲ)$\frac{{m}_{0}g}{a}$;(4)0.200.
点评 本题考查了牛顿第二定律的应用,应用匀变速直线运动的推论、牛顿第二定律即可解题,要熟练掌握基础知识,在平时练习中要加强基础知识的理解与应用.

| A. | 该衰变方程为${\;}_{88}^{228}$Ra→${\;}_{86}^{224}$Rn+${\;}_{2}^{4}$He | |
| B. | 若该元素的半衰期为T,则经过2T的时间,2kg的${\;}_{88}^{228}$Ra中有1.5kg已经发生了衰变 | |
| C. | 随着该元素样品的不断衰变,剩下未衰变的原子核${\;}_{88}^{228}$Ra越来越少,其半衰期也变短 | |
| D. | 若把该元素放到密闭容器中,则可以减慢它的衰变速度 | |
| E. | 该元素的半衰期不会随它所处的物理环境、化学状态的变化而变化 |
 如图甲所示.细线下悬挂一个除去了柱塞的注射器.注射器可在竖直面内摆动.且在摆动过程中能持续向下流出一细束墨水.沿着与注射器摆动平面垂直的方向匀速拖动一张硬纸板,摆动的注射器流出的墨水在硬纸板上形成了如图乙所示的曲线.注射器喷嘴到硬纸板的距离很小.开始时注射器中装满墨水,最终墨水全都流尽.若按图乙所示建立xOy′坐标系,则硬纸板上的墨迹所呈现的图样可视为注射器振动的图象.关于图乙所示的图象.下列说法中正确的是( )
如图甲所示.细线下悬挂一个除去了柱塞的注射器.注射器可在竖直面内摆动.且在摆动过程中能持续向下流出一细束墨水.沿着与注射器摆动平面垂直的方向匀速拖动一张硬纸板,摆动的注射器流出的墨水在硬纸板上形成了如图乙所示的曲线.注射器喷嘴到硬纸板的距离很小.开始时注射器中装满墨水,最终墨水全都流尽.若按图乙所示建立xOy′坐标系,则硬纸板上的墨迹所呈现的图样可视为注射器振动的图象.关于图乙所示的图象.下列说法中正确的是( )| A. | x轴表示拖动硬纸板的速度 | |
| B. | y轴表示注射器离最低点的高度 | |
| C. | 注射器振动的周期先变大后变小 | |
| D. | 匀速拖动硬纸板移动距离L的时间等于注射器挥动的周期 |
 如图所示.质量均为M=0.4kg的两长平板小车A和B开始时紧靠在一起都静止于光滑水平面上.小物块(可看成质点)m=0.2kg以初速度v=9m/s从最左端滑上A小车的上表面,最后停在B小车最右端时速度为v2=2m/s,最后A的速度v1为.( )
如图所示.质量均为M=0.4kg的两长平板小车A和B开始时紧靠在一起都静止于光滑水平面上.小物块(可看成质点)m=0.2kg以初速度v=9m/s从最左端滑上A小车的上表面,最后停在B小车最右端时速度为v2=2m/s,最后A的速度v1为.( )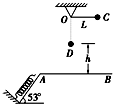 如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为53°的光滑斜面上.一长为L=9cm的轻质细绳一端固定在O点,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球在位置C由静止释放,小球到达最低点D时,细绳刚好被拉断.之后小球在运动过程中恰好沿斜面方向将弹簧压缩,最大压缩量为x=5cm.(g=10m/s2,sin 53°=0.8,cos 53°=0.6)求:
如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为53°的光滑斜面上.一长为L=9cm的轻质细绳一端固定在O点,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球在位置C由静止释放,小球到达最低点D时,细绳刚好被拉断.之后小球在运动过程中恰好沿斜面方向将弹簧压缩,最大压缩量为x=5cm.(g=10m/s2,sin 53°=0.8,cos 53°=0.6)求: 玻璃砖的顶角为直角,如图所示,一束光线从空气中斜射入玻璃砖一个侧面,进而偏折到另一个侧面,已知该玻璃砖的折射率为2
玻璃砖的顶角为直角,如图所示,一束光线从空气中斜射入玻璃砖一个侧面,进而偏折到另一个侧面,已知该玻璃砖的折射率为2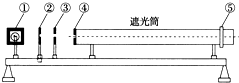 如图为双缝干涉测光波长的实验设备示意图.
如图为双缝干涉测光波长的实验设备示意图.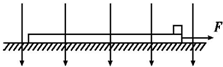 如图所示,长L=1.6m,质量M=3kg的木板静止放在光滑水平面上,质量m=1kg、带电荷量q=+2.5×10-4C的小物块放在木板的右端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向竖直向下,电场强度为E=4.0×104N/C的匀强电场,现对木板施加一水平向右的拉力F.取g=10m/s2,最大静摩擦力等于滑动摩擦力,求:
如图所示,长L=1.6m,质量M=3kg的木板静止放在光滑水平面上,质量m=1kg、带电荷量q=+2.5×10-4C的小物块放在木板的右端,木板和物块间的动摩擦因数μ=0.1,所在空间加有一个方向竖直向下,电场强度为E=4.0×104N/C的匀强电场,现对木板施加一水平向右的拉力F.取g=10m/s2,最大静摩擦力等于滑动摩擦力,求: