题目内容
如图甲所示,在PQ左侧空间有方向斜向右上的匀强电场E1在PQ右侧空间 有一竖直向上的匀强电场E2=0.4N/C,还有垂直纸面向里的匀强磁场B(图甲中未画 出)和水平向右的匀强电场E3(图甲中未画出),B和E3随时间变化的情况如图乙所 示,MN为距PQ边界2.295m的竖直墙壁,现有一带正电的微粒质量为4x1O-7kg电量为1xlO-5C,从左侧电场中距PQ边界
m的A处无初速释放后,沿直线以1m/s速度垂直PQ边界进入右侧场区,设进入右侧场时刻t=0,取g=lOm/s2.求: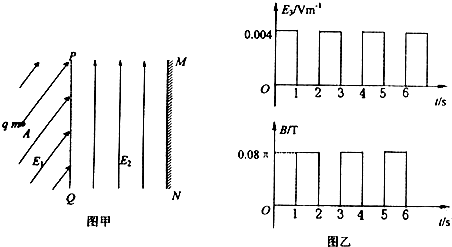
(1)PQ左侧匀强电场的电场强度E1,的大小及方向.(sin37°=0.6);
(2)带电微粒在PQ右侧场区中运动了1.5s时的速度的大小及方向;
(3)带电微粒在PQ右侧场区中运动多长时间与墙壁碰撞?(
≈0.19)
| 1 |
| 15 |

(1)PQ左侧匀强电场的电场强度E1,的大小及方向.(sin37°=0.6);
(2)带电微粒在PQ右侧场区中运动了1.5s时的速度的大小及方向;
(3)带电微粒在PQ右侧场区中运动多长时间与墙壁碰撞?(
| 1.2 |
| 2π |
分析:(1)带电粒子在匀强电场和重力场中的运动,对微粒进行受力分析,根据牛顿第二定律,运用正交分解法列式,即可求解.
(2)首先要判定微粒的重力和电场力E2q是一对平衡力,然后分析在不同的时间段内微粒的受力情况和运动情况,即可根据牛顿第二定律和运动学公式结合解答.
(3)要先计算出在0~1s时间内带电微粒前进距离和带电微粒在磁场B中作圆周运动的半径,判定微粒在第一个周期内是否会打在墙壁上,若不能,再计算出在2s~3s时间内带电微粒前进距离和带电微粒在磁场B中作圆周运动的半径,判定微粒在第二个周期内是否会打在墙壁上,判定的结果是能够打在墙壁上,画出轨迹图象,即可做出正确的判定,并根据运动学公式求解时间.
(2)首先要判定微粒的重力和电场力E2q是一对平衡力,然后分析在不同的时间段内微粒的受力情况和运动情况,即可根据牛顿第二定律和运动学公式结合解答.
(3)要先计算出在0~1s时间内带电微粒前进距离和带电微粒在磁场B中作圆周运动的半径,判定微粒在第一个周期内是否会打在墙壁上,若不能,再计算出在2s~3s时间内带电微粒前进距离和带电微粒在磁场B中作圆周运动的半径,判定微粒在第二个周期内是否会打在墙壁上,判定的结果是能够打在墙壁上,画出轨迹图象,即可做出正确的判定,并根据运动学公式求解时间.
解答: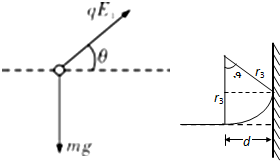 解:(1)设PQ左侧匀强电场场强为E1,方向与水平方向夹角为θ.
解:(1)设PQ左侧匀强电场场强为E1,方向与水平方向夹角为θ.
沿水平方向有:qE1cosθ=ma
沿竖直方向有:qE1sinθ=mg
对水平方向的匀加速运动有:v2=2as
代入数据可解得:E1=0.5N/C,θ=53°
即E1大小为0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在PQ右侧场区始终满足:qE2=mg
在0~1s时间内,带电微粒在E3电场中a=
=
m/s2=0.1m/s2
带电微粒在1s时的速度大小为 v1=v+at=(1+0.1×1)m/s=1.1m/s
在1~1.5s时间内,带电微粒在磁场B中运动,周期为T=
=
s=1s;
在1~1.5s时间内,带电微粒在磁场B中正好作半个圆周运动.所以带电微粒在PQ右侧场区中运动了1.5s时的速度大小为1.1m/s,方向水平向左.
(3)在0s~1s时间内带电微粒前进距离
s1=vt1+
at12=1×1+
×0.1×12m=1.05m
带电微粒在磁场B中作圆周运动的半径 r1=
=
m=
m
因为r+s1<2.295m,所以在1s~2s时间内带电微粒未碰及墙壁.
在2s~3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2
在3s内带电微粒共前进距离
s3=vt3+
a
=(1×2+
×0.1×22)m=2.2m,
在3s时带电微粒的速度大小为 v3=v+at3=(1+0.1×2)m/s=1.2m/s;
在3s~4s时间内带电微粒在磁场B中作圆周运动的半径 r3=
=
=
m=0.19m;
因为r3+s3>2.295m,所以在4s时间内带电微粒碰及墙壁.
带电微粒在3s以后运动情况如图,
其中 d=(2.295-2.2)m=0.095m;
sinθ=
=0.5,θ=30°;
所以,带电微粒作圆周运动的时间为t3=
=
=
s=
s
带电微粒与墙壁碰撞的时间为 t总=(3+
)s=
s.
答:
(1)PQ左侧匀强电场的电场强度E1的大小0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在PQ右侧场区中运动了1.5s时的速度的大小1.1m/s,方向水平向左.
(3)带电微粒在PQ右侧场区中运动
s时间与墙壁碰撞.
 解:(1)设PQ左侧匀强电场场强为E1,方向与水平方向夹角为θ.
解:(1)设PQ左侧匀强电场场强为E1,方向与水平方向夹角为θ. 沿水平方向有:qE1cosθ=ma
沿竖直方向有:qE1sinθ=mg
对水平方向的匀加速运动有:v2=2as
代入数据可解得:E1=0.5N/C,θ=53°
即E1大小为0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在PQ右侧场区始终满足:qE2=mg
在0~1s时间内,带电微粒在E3电场中a=
| qE3 |
| m |
| 1×10-5×0.004 |
| 4×10-7 |
带电微粒在1s时的速度大小为 v1=v+at=(1+0.1×1)m/s=1.1m/s
在1~1.5s时间内,带电微粒在磁场B中运动,周期为T=
| 2πm |
| qB |
| 2π×4×10-7 |
| 1×10-5×0.08π |
在1~1.5s时间内,带电微粒在磁场B中正好作半个圆周运动.所以带电微粒在PQ右侧场区中运动了1.5s时的速度大小为1.1m/s,方向水平向左.
(3)在0s~1s时间内带电微粒前进距离
s1=vt1+
| 1 |
| 2 |
| 1 |
| 2 |
带电微粒在磁场B中作圆周运动的半径 r1=
| mv |
| qB |
| 4×10-7×1.1 |
| 1×10-5×0.08π |
| 1.1 |
| 2π |
因为r+s1<2.295m,所以在1s~2s时间内带电微粒未碰及墙壁.
在2s~3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2
在3s内带电微粒共前进距离
s3=vt3+
| 1 |
| 2 |
| t | 2 3 |
| 1 |
| 2 |
在3s时带电微粒的速度大小为 v3=v+at3=(1+0.1×2)m/s=1.2m/s;
在3s~4s时间内带电微粒在磁场B中作圆周运动的半径 r3=
| mv3 |
| qB |
| 4×10-7×1.2 |
| 1×10-5×0.08π |
| 1.2 |
| 2π |
因为r3+s3>2.295m,所以在4s时间内带电微粒碰及墙壁.
带电微粒在3s以后运动情况如图,
其中 d=(2.295-2.2)m=0.095m;
sinθ=
| d |
| r3 |
所以,带电微粒作圆周运动的时间为t3=
| T3 |
| 12 |
| 2πm |
| 12qB |
| 2π×4×10-7 |
| 12×1×10-5×0.08π |
| 1 |
| 12 |
带电微粒与墙壁碰撞的时间为 t总=(3+
| 1 |
| 12 |
| 37 |
| 12 |
答:
(1)PQ左侧匀强电场的电场强度E1的大小0.5N/C,方向与水平向右方向夹53°角斜向上.
(2)带电微粒在PQ右侧场区中运动了1.5s时的速度的大小1.1m/s,方向水平向左.
(3)带电微粒在PQ右侧场区中运动
| 37 |
| 12 |
点评:本题考查带电微粒在电场和磁场中的运动,情景复杂,在解答的过程中,关键要对各种情景有非常清晰的判断,才能理清头绪,正确作答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
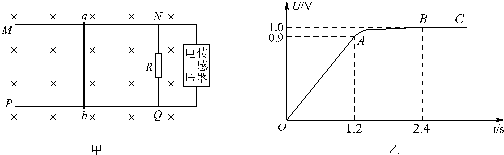
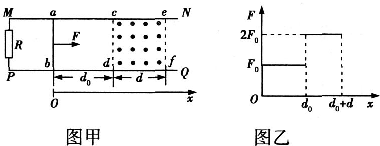 如图甲所示,光滑的平行水平金属导轨MN、PQ相距L,在MP之间接一个阻值为R的电阻,在两导轨间cdfe矩形区域内有垂直导轨平面竖直向上、宽为d的匀强磁场,磁感应强度为B.一质量为m、电阻为r、长度也刚好为L的导体棒ab垂直搁在导轨上,与磁场左边界相距d0.现用一个水平向右的力F拉棒ab,使它由静止开始运动,棒ab离开磁场区域前已做匀速直线运动,棒ab与导轨始终保持良好接触,导轨电阻不计,F随ab与初始位置的距离x变化的情况如图乙所示,F0已知.下列判断正确的是( )
如图甲所示,光滑的平行水平金属导轨MN、PQ相距L,在MP之间接一个阻值为R的电阻,在两导轨间cdfe矩形区域内有垂直导轨平面竖直向上、宽为d的匀强磁场,磁感应强度为B.一质量为m、电阻为r、长度也刚好为L的导体棒ab垂直搁在导轨上,与磁场左边界相距d0.现用一个水平向右的力F拉棒ab,使它由静止开始运动,棒ab离开磁场区域前已做匀速直线运动,棒ab与导轨始终保持良好接触,导轨电阻不计,F随ab与初始位置的距离x变化的情况如图乙所示,F0已知.下列判断正确的是( )| A、棒ab在ac之间的运动是匀加速直线运动 | ||
| B、棒ab在ce之间可能先做加速度减小的运动,再做匀速运动 | ||
| C、棒ab在ce之间不可能一直做匀速运动 | ||
D、棒ab经过磁场的过程中,通过电阻R的电荷量为
|