题目内容
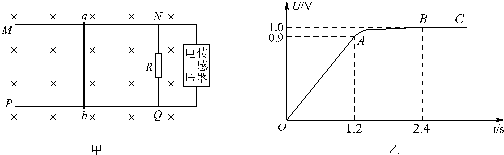
如图甲所示，MN、PQ是固定于同一水平面内相互平行的粗糙长直导轨，间距L=2.0m，R是连在导轨一端的电阻，质量m=1.0kg的导体棒ab垂直跨在导轨上，电压传感器与这部分装置相连．导轨所在空间有磁感应强度B=0.50T、方向竖直向下的匀强磁场．从t=0开始对导体棒ab施加一个水平向左的拉力，使其由静止开始沿导轨向左运动，电压传感器测出R两端的电压随时间变化的图线如图乙所示，其中OA、BC段是直线，AB段是曲线．假设在1.2s以后拉力的功率P=4.5W保持不变．导轨和导体棒ab的电阻均可忽略不计，导体棒ab在运动过程中始终与导轨垂直，且接触良好．不计电压传感器对电路的影响．g取10m/s2．求：
（1）导体棒ab最大速度vm的大小；
（2）在1.2s～2.4s的时间内，该装置总共产生的热量Q；
（3）导体棒ab与导轨间的动摩擦因数μ和电阻R的值．
（1）导体棒ab最大速度vm的大小；
（2）在1.2s～2.4s的时间内，该装置总共产生的热量Q；
（3）导体棒ab与导轨间的动摩擦因数μ和电阻R的值．
分析：（1）当感应电动势最大时，速度最大，从乙图中读出最大电压，根据E=BLv即可求解；
（2）根据E=BLv可知在0～1.2s内导体棒做匀加速直线运动，求出t1=1.2s时导体棒的速度，在1.2s～2.4s时间内，根据功能原理即可求解；
（3）求出导体棒做匀加速运动的加速度，根据P=Fv，求出t=1.2s和2.4s时的拉力，根据牛顿第二定律、欧姆定律及安培力公式，联立方向即可求解．
（2）根据E=BLv可知在0～1.2s内导体棒做匀加速直线运动，求出t1=1.2s时导体棒的速度，在1.2s～2.4s时间内，根据功能原理即可求解；
（3）求出导体棒做匀加速运动的加速度，根据P=Fv，求出t=1.2s和2.4s时的拉力，根据牛顿第二定律、欧姆定律及安培力公式，联立方向即可求解．
解答：
解：（1）从乙图可知，t=2.4s时R两端的电压达到最大，Um=1.0V，由于导体棒内阻不计，故Um=Em=BLvm=1.0V，
所以 vm=
=1m/s ①
（2）因为E=U=BLv，而B、L为常数，所以，在0～1.2s内导体棒做匀加速直线运动．设导体棒在这段时间内加速度为a．设t1=1.2s时导体棒的速度为v1，由乙图可知此时电压U1=0.90V．
因为 E1=U1=BLv1 ②
所以v1=
=0.9m/s
在1.2s～2.4s时间内，根据功能原理
mv12+P?△t=
mvm2+Q③
所以 Q=5.3J
（3）导体棒做匀加速运动的加速度
a=
=0.75m/s2
当t=1.2s时，设拉力为F1，则有
F1=
=5N
同理，设t=2.4s时拉力为F2，则有
F2=
=4.5N
根据牛顿第二定律有
F1-f-F安1=ma④
F2-f-F安2=0⑤
mg-N=0⑥
又因为 F安1=BI1L=
⑦
F安2=BI2L=
⑧
f=μN⑨
由④⑤⑥⑦⑧⑨，代入数据可求得：
R=0.4Ω，μ=0.2
答：（1）导体棒ab最大速度vm的大小为1m/s；
（2）在1.2s～2.4s的时间内，该装置总共产生的热量Q为5.3J；
（3）导体棒ab与导轨间的动摩擦因数μ为0.2；电阻R的值为0.4Ω．
解：（1）从乙图可知，t=2.4s时R两端的电压达到最大，Um=1.0V，由于导体棒内阻不计，故Um=Em=BLvm=1.0V，所以 vm=
| Em |
| BL |
（2）因为E=U=BLv，而B、L为常数，所以，在0～1.2s内导体棒做匀加速直线运动．设导体棒在这段时间内加速度为a．设t1=1.2s时导体棒的速度为v1，由乙图可知此时电压U1=0.90V．
因为 E1=U1=BLv1 ②
所以v1=
| U1 |
| BL |
在1.2s～2.4s时间内，根据功能原理
| 1 |
| 2 |
| 1 |
| 2 |
所以 Q=5.3J
（3）导体棒做匀加速运动的加速度
a=
| v1-0 |
| t |
当t=1.2s时，设拉力为F1，则有
F1=
| P |
| v1 |
同理，设t=2.4s时拉力为F2，则有
F2=
| P |
| vm |
根据牛顿第二定律有
F1-f-F安1=ma④
F2-f-F安2=0⑤
mg-N=0⑥
又因为 F安1=BI1L=
| BLU1 |
| R |
F安2=BI2L=
| BLU2 |
| R |
f=μN⑨
由④⑤⑥⑦⑧⑨，代入数据可求得：
R=0.4Ω，μ=0.2
答：（1）导体棒ab最大速度vm的大小为1m/s；
（2）在1.2s～2.4s的时间内，该装置总共产生的热量Q为5.3J；
（3）导体棒ab与导轨间的动摩擦因数μ为0.2；电阻R的值为0.4Ω．
点评：本题是电磁感应与电路、力学知识的综合，首先要识别电路的结构，把握路端电压与电动势的关系，而电动势是联系电路与电磁感应的桥梁，可得到速度的表达式；安培力是联系力与电磁感应的纽带，难度较大．
练习册系列答案
相关题目
如图甲所示，MN为一原来不带电的导体棒，q为一带电量恒定的点电荷，当达到静电平衡后，导体棒上的感应电荷在棒内P点处产生的场强大小为E1，p点的电势为U1．现用一导线将导体棒的N端接地，其它条件不变，如图乙所示，待静电平衡后，导体棒上的感应电荷在棒内P点处产生的场强为E2，P点的电势为U2，则（ ）
如图甲所示，MN为很大的薄金属板（可理解为无限大），金属板原来不带电．在金属板的右侧，距金属板距离为d的位置上放入一个带正电、电荷量为q的点电荷，由于静电感应产生了如图甲所示的电场分布．P是点电荷右侧，与点电荷之间的距离也为d的一个点，几位同学想求出P点的电场强度大小，但发现问题很难．几位同学经过仔细研究，从图乙所示的电场得到了一些启示，经过查阅资料他们知道：图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的．图乙中两异号点电荷电荷量的大小均为q，它们之间的距离为2d，虚线是两点电荷连线的中垂线．由此他们分别求出了P点的电场强度大小，一共有以下四个不同的答案（k为静电力常量），其中正确的是（ ）