题目内容
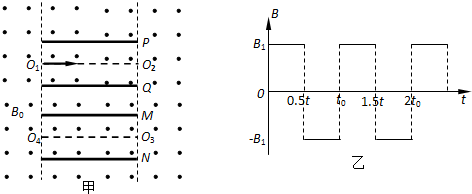
(2013?威海模拟)如图甲所示,两个完全相同的平行板电容器PQ和MN,板间距离为d,极板长为L,极板厚度不计.将它们置于图示方向足够大的匀强磁场中,磁感应强度为B0,两电容器极板的左端和右端分别对齐,两电容器极板所加电压值相同.一质量为m、电荷量为+q、重力不计的粒子从极板P、Q间的中轴线O1O2左边缘的O1点,以速度v0沿O1O2匀速穿过电容器PQ,经过磁场偏转后沿极板M、N的中轴线O3O4做匀速直线运动,又经过磁场回到O1点,如此循环往复.不计电容器之外的电场对粒子运动的影响.求:
(1)极板P、Q,M、N间所加电压的数值U.
(2)Q板和M板间的距离x.
(3)粒子从O1点开始运动到再次回到O1点所用的时间.
(4)若撤去电容器上所加的电压,将原磁场换作按图乙规律变化的磁场,取垂直纸面向里为磁场的正方向.粒子仍从O1点沿O1O2在0时刻以速度v0进入电容器PQ,在t0时刻恰好从P板右边缘水平射出(t0为未知量).则B1为多少?
(1)极板P、Q,M、N间所加电压的数值U.
(2)Q板和M板间的距离x.
(3)粒子从O1点开始运动到再次回到O1点所用的时间.
(4)若撤去电容器上所加的电压,将原磁场换作按图乙规律变化的磁场,取垂直纸面向里为磁场的正方向.粒子仍从O1点沿O1O2在0时刻以速度v0进入电容器PQ,在t0时刻恰好从P板右边缘水平射出(t0为未知量).则B1为多少?

分析:(1)正电荷在PQ间做匀速直线运动,受洛伦兹力和电场力,根据平衡条件列式;然后根据U=Ed列式;最后联立求解;
(2)正电荷在磁场中做匀速圆周运动时,由洛伦兹力提供向心力,列式求得轨迹的半径,即可由几何关系得到x应满足的条件;
(3)粒子运动一周,先根据T=
和t=
T求解磁场中运动时间;再根据t=
求解复合场中运动的时间;最后相加即可;
(4)画出运动轨迹,结合几何关系求解出轨道半径;然后根据洛伦兹力提供向心力列式,求解出磁感应强度.
(2)正电荷在磁场中做匀速圆周运动时,由洛伦兹力提供向心力,列式求得轨迹的半径,即可由几何关系得到x应满足的条件;
(3)粒子运动一周,先根据T=
| 2πm |
| qB |
| θ |
| 2π |
| 2L |
| v0 |
(4)画出运动轨迹,结合几何关系求解出轨道半径;然后根据洛伦兹力提供向心力列式,求解出磁感应强度.
解答:解:(1)做匀速直线运动时,正电荷受到的电场力与受到的磁场力平衡,有:
qE=qv0B1
匀强电场中:
E=
则:U=B0v0d;
(2)电荷在磁场中的运动:
qv0B0=m
则正电荷做圆周运动的半径为:
r=
x=2r-d
则:x=
-d;
(3)由公式T=
得:
T=
粒子在磁场中运动的总时间为:
t1=T=
粒子在两平行板间运动的总时间为:
t2=2
粒子运动的总时间为: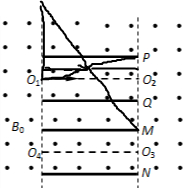
t=t1+t2=
+
;
(4)由几何知识可知:
=(r1-
)2+(
)2
又洛伦兹力提供向心力,有:
qv0B1=m
联立解得:B1=
;
答:(1)极板P、Q,M、N间所加电压的数值U为B0v0d.
(2)Q板和M板间的距离x为
-d.
(3)粒子从O1点开始运动到再次回到O1点所用的时间为
+
.
(4)B1为
.
qE=qv0B1
匀强电场中:
E=
| U |
| d |
则:U=B0v0d;
(2)电荷在磁场中的运动:
qv0B0=m
| ||
| r |
则正电荷做圆周运动的半径为:
r=
| mv0 |
| qB0 |
x=2r-d
则:x=
| 2mv0 |
| qB 0 |
(3)由公式T=
| 2πr |
| v0 |
T=
| 2πm |
| qB0 |
粒子在磁场中运动的总时间为:
t1=T=
| 2πm |
| qB0 |
粒子在两平行板间运动的总时间为:
t2=2
| L |
| v0 |
粒子运动的总时间为:

t=t1+t2=
| 2πm |
| qB0 |
| 2L |
| v0 |
(4)由几何知识可知:
| r | 2 1 |
| d |
| 4 |
| L |
| 2 |
又洛伦兹力提供向心力,有:
qv0B1=m
| ||
| r1 |
联立解得:B1=
| 8mv0d |
| q(d2+4L2) |
答:(1)极板P、Q,M、N间所加电压的数值U为B0v0d.
(2)Q板和M板间的距离x为
| 2mv0 |
| qB 0 |
(3)粒子从O1点开始运动到再次回到O1点所用的时间为
| 2πm |
| qB0 |
| 2L |
| v0 |
(4)B1为
| 8mv0d |
| q(d2+4L2) |
点评:本题关键是明确粒子的运动规律,然后分匀速圆周运动和匀速直线运动阶段进行讨论,不难.

练习册系列答案
相关题目
 (2013?威海模拟)质量相等的两个质点A、B在拉力作用下从同一地点沿同一直线竖直向上运动的v-t图象如图所示,下列说法正确的是( )
(2013?威海模拟)质量相等的两个质点A、B在拉力作用下从同一地点沿同一直线竖直向上运动的v-t图象如图所示,下列说法正确的是( ) (2013?威海模拟)如图所示,在粗糙水平面上放着一个三角形木块abc,在它的两个粗糙斜面上分别放有质量为m1和m2的两个物体,已知m1>m2,θ1<θ2.若两物体都与三角形木块保持相对静止,以下说法正确的是( )
(2013?威海模拟)如图所示,在粗糙水平面上放着一个三角形木块abc,在它的两个粗糙斜面上分别放有质量为m1和m2的两个物体,已知m1>m2,θ1<θ2.若两物体都与三角形木块保持相对静止,以下说法正确的是( ) 为理想表,设灯泡电阻为定值,额定电压为15V,刚开始时滑动触头P位于C位置.下列说法正确的是( )
为理想表,设灯泡电阻为定值,额定电压为15V,刚开始时滑动触头P位于C位置.下列说法正确的是( )
 (2013?威海模拟)如图甲所示,水平面上两根足够长的金属导轨平行固定放置,间距为L,一端通过导线与阻值为R的电阻连接.导轨上放一质量为m的金属杆,金属杆、导轨的电阻均忽略不计,匀强磁场垂直导轨平面向下.用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动.当改变拉力的大小时,相对应的匀速运动速度v也会变化,v和F的关系如图乙所示.下列说法正确的是( )
(2013?威海模拟)如图甲所示,水平面上两根足够长的金属导轨平行固定放置,间距为L,一端通过导线与阻值为R的电阻连接.导轨上放一质量为m的金属杆,金属杆、导轨的电阻均忽略不计,匀强磁场垂直导轨平面向下.用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动.当改变拉力的大小时,相对应的匀速运动速度v也会变化,v和F的关系如图乙所示.下列说法正确的是( )