Question

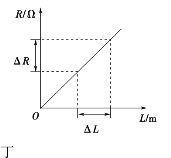
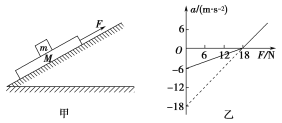
【题目】如图甲所示，一质量为M的长木板静置于光滑的斜面上，其上放置一质量为m的小滑块，斜面倾角θ＝，木板受到沿斜面向上拉力F作用时，用传感器测出长木板的加速度a与力F的关系如图乙所示，重力加速度取g＝10m/s2，sin＝0.6，cos＝0.8。求：

(1)小滑块与木板的动摩擦因数为多少？

(2)当拉力F＝20N时，长木板的加速度大小为多大？

Answer 1

【答案】(1)0.75(2)2m/s2

【解析】

(1)当F等于18N时，加速度为a＝0。对整体由平衡条件：

F＝(M＋m)gsinθ

代入数据解得

M＋m＝3kg

当F大于18N时，根据牛顿第二定律得

F－Mgsinθ－μmgcosθ＝Ma

长木板的加速度

a＝F－gsinθ－

知图线的斜率

k＝＝1

截距

b＝-gsinθ-＝-18

解得

M＝1kg，m＝2kg，μ＝0.75

(2)当拉力F＝20N时，代入长木板的加速度

a＝F－gsinθ－

解得长木板的加速度为

a1＝2m/s2