题目内容
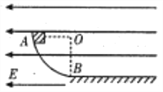
【题目】一轻绳一端连接一小球，另一端固定在悬点上．开始时小球静止在最低点， 一方向水平的冲力作用到小球上使小球立刻获得一个水平速度 v1 ，结果小球在竖直面内来回摆动，如图中①．此后，当小球某次摆至最高点时，又有另一方向水平的冲力作用到小球上使小球立刻获得另一个水平速度 v2 ，此后小球在水平面内做匀速圆周运动，如图中②，而且运动过程中绳子的拉力大小与前面小球在摆动过程中绳子拉力的最大值相等．求：
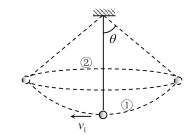
（1）轻绳偏离竖直方向的最大夹角θ．
（2）速度
和速度
大小的比值
【答案】（1）600（2）
【解析】设小球质量为m，绳子长度为l．小球摆动过程机械能守恒，则： 
mv12=mgl（1-cosθ）
小球在最低点时绳子拉力最大Fm-mg=m
联立解得：Fm=mg（3-2cosθ）
小球在水平面内做匀速圆周运动，有Fm=mgtanθ=m
圆周半径：r=lsinθ
设绳子拉力为F，则mg=Fcosθ
又由题意可得：Fm=F
联立以上各式解得：cosθ=0.5，即θ=600； 
．
练习册系列答案
口算能手系列答案
相关题目
