题目内容
4.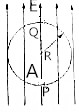 如图所示,质量为m、半径为R的圆形光滑绝缘轨道固定在竖直平面内,在轨道所在平面加一竖直向上的匀强电场,P,Q两点分别为圆形轨道的最低点和最高点,在P点静止放置一个质量为m、电荷为q的带正电的小球A(不计空气阻力,重力加速度为g)
如图所示,质量为m、半径为R的圆形光滑绝缘轨道固定在竖直平面内,在轨道所在平面加一竖直向上的匀强电场,P,Q两点分别为圆形轨道的最低点和最高点,在P点静止放置一个质量为m、电荷为q的带正电的小球A(不计空气阻力,重力加速度为g)(1)若小球A以速度v0在竖直平面内沿圆形轨道做匀速圆周运动,求匀强电场的电场强度E及小球运动至Q点时对轨道的压力FQ;
(2)现使匀强电场的场强大小变为原来的2倍,方向不变,且将小球A置于轨道最高点Q,给小球A一个水平初速度v1,使它沿圆形轨道运动且不脱离轨道,那么初速度v1应满足什么条件.
分析 小球A以速度v0在竖直平面内沿圆形轨道做匀速圆周运动,电场力等于重力;结合牛顿第二定律与向心力表达式,求解压力FQ,结合牛顿第二定律与向心力表达式,从而即可求解.
解答 解:
(1)小球A以速度v0在竖直平面内沿圆形轨道做匀速圆周运动,电场力等于重力;
即qE=mg
E=$\frac{mg}{q}$
牛顿第二定律与向心力表达式 N=m$\frac{{v}_{0}^{2}}{R}$
由牛顿第三定律,得 FQ=N=m$\frac{{v}_{0}^{2}}{R}$
(2)现使匀强电场的场强大小变为原来的2倍,方向不变,牛顿第二定律与向心力表达式
N+mg-2qE=m$\frac{{v}_{1}^{2}}{R}$
当电场力大于重力时,由动能定理:-4qER+2mgR=$\frac{1}{2}$mvp2-$\frac{1}{2}$mv12…①
小球恰能通过p点时,-mg+2qE=m$\frac{{v}_{p}^{2}}{R}$…②$\frac{{v}_{0}^{2}}{R}$
联立①②解得:v1=$\sqrt{5gR}$;
所以要使小球能通过P点v1≥$\sqrt{5gR}$;
答:(1)匀强电场的电场强度$\frac{mg}{q}$;及小球运动至Q点时对轨道的压力FQ=m$\frac{{v}_{0}^{2}}{R}$
(2)初速度v1应满足条件v1≥$\sqrt{5gR}$;
点评 考查动能定理与牛顿第二、三定律的应用,掌握谁提供向心力是解题的关键,同时注意力做功的正负

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
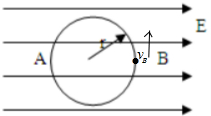
14.如图所示,半径为r的绝缘细圆环的环面固定在水平面上,一电荷量为-q、质量为m的小球穿在环上,可沿环做无摩擦的圆周运动.该空间存在看与环面平行的匀强电场,电场强度大小为$\frac{mg}{4q}$,若小球经B点时,速度VB的方向恰与电场垂直,且圆环与小球间沿水平方向无力的作用,那么下列说法中正确的是( )

| A. | 小球经过B点时.速度VB的大小为$\sqrt{gr}$ | |
| B. | 小球经过B点时.速度VB的大小为$\frac{1}{2}\sqrt{gr}$ | |
| C. | 小球经过A点(与B点关于圆心O对称)时对环在水平方向的作用力大小为1.5mg | |
| D. | 小球经过A点(与B点关于圆心O对称)时对环在水平方向的作用力大小为2mg |
20.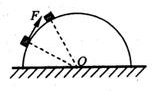 如图,表面光滑的半球体固定在水平面上,O为球心,一小物体在拉力F的作用下,缓慢地沿球面向上运动一小段距离,在物块运动过程中F始终沿球面的切线方向,球面对物块的弹力大小用FN表示.在运动过程中( )
如图,表面光滑的半球体固定在水平面上,O为球心,一小物体在拉力F的作用下,缓慢地沿球面向上运动一小段距离,在物块运动过程中F始终沿球面的切线方向,球面对物块的弹力大小用FN表示.在运动过程中( )
 如图,表面光滑的半球体固定在水平面上,O为球心,一小物体在拉力F的作用下,缓慢地沿球面向上运动一小段距离,在物块运动过程中F始终沿球面的切线方向,球面对物块的弹力大小用FN表示.在运动过程中( )
如图,表面光滑的半球体固定在水平面上,O为球心,一小物体在拉力F的作用下,缓慢地沿球面向上运动一小段距离,在物块运动过程中F始终沿球面的切线方向,球面对物块的弹力大小用FN表示.在运动过程中( )| A. | F减小,FN增大 | B. | F减小,FN减小 | C. | F增大,FN增大 | D. | F增大,FN减小 |
9.有两个物体P和Q,其质量分别为mP和mQ,且mP<mQ,分别受到恒力FP和FQ的作用,由静止开始运动,经过相同的时间,动能相同,它们的加速度分别为aP和aQ,则( )
| A. | FP>FQ且aP<aQ | B. | FP>FQ且aP>aQ | C. | FP<FQ且aP>aQ | D. | FP<FQ且aP<aQ OBA |
16.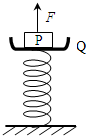 如图所示,一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为一重物.已知P的质量M=10kg,Q的质量m=2kg,弹簧质量不计,系统处于静止,g=10m/s2.现给P施加一个竖直向上的力F=120N的瞬间,P对Q的压力大小( )
如图所示,一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为一重物.已知P的质量M=10kg,Q的质量m=2kg,弹簧质量不计,系统处于静止,g=10m/s2.现给P施加一个竖直向上的力F=120N的瞬间,P对Q的压力大小( )
 如图所示,一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为一重物.已知P的质量M=10kg,Q的质量m=2kg,弹簧质量不计,系统处于静止,g=10m/s2.现给P施加一个竖直向上的力F=120N的瞬间,P对Q的压力大小( )
如图所示,一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为一重物.已知P的质量M=10kg,Q的质量m=2kg,弹簧质量不计,系统处于静止,g=10m/s2.现给P施加一个竖直向上的力F=120N的瞬间,P对Q的压力大小( )| A. | 100N | B. | 80N | C. | 20N | D. | 0N |
13.物体沿一直线做匀加速直线运动,已知它在第2s内的位移为4.0m,第3s内的位移为6.0m,则下列说法错误的是( )
| A. | 第2s末的速度为5m/s | B. | 第1s内的位移是2.0m | ||
| C. | 加速度大小是2.0m/s | D. | 初速度为零 |
 如图甲所示,竖直放置的直角三角形NMP(MP边处于水平),∠NMP=θ,MP中点处固定一电量为Q的正点电荷,MN是长为a的光滑绝缘杆,杆上穿有一带正电的小球(可视为点电荷),小球自N点由静止释放,小球的重力势能和电势能随位置x(取M点处x=0)的变化图象如图乙所示(图中E0、E1、E2为已知量),重力加速度为g,设无限远处电势为零,M点所处的水平面为重力零势能面.
如图甲所示,竖直放置的直角三角形NMP(MP边处于水平),∠NMP=θ,MP中点处固定一电量为Q的正点电荷,MN是长为a的光滑绝缘杆,杆上穿有一带正电的小球(可视为点电荷),小球自N点由静止释放,小球的重力势能和电势能随位置x(取M点处x=0)的变化图象如图乙所示(图中E0、E1、E2为已知量),重力加速度为g,设无限远处电势为零,M点所处的水平面为重力零势能面.