题目内容
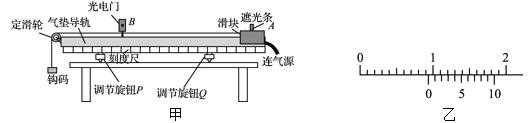
【题目】在某电视台举办的冲关游戏中,AB是处于竖直平面内的光滑圆弧轨道,半径R=1.6m,BC是长度为L1=3m的水平传送带,CD是长度为L2=3.6m水平粗糙轨道,AB、CD轨道与传送带平滑连接,参赛者抱紧滑板从A处由静止下滑,参赛者和滑板可视为质点,参赛者质量m=60kg,滑板质量可忽略.已知滑板与传送带、水平轨道的动摩擦因数分别为μ1=0.4、μ2=0.5,g取10m/s2.求:
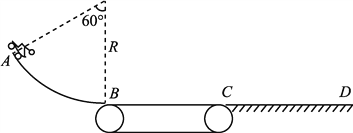
(1)参赛者运动到圆弧轨道B处对轨道的压力;
(2)若参赛者恰好能运动至D点,求传送带运转速率及方向;
(3)在第(2)问中,传送带由于传送参赛者多消耗的电能.
【答案】(1)1200N,方向竖直向下(2)顺时针运转,v=6m/s(3)720J
【解析】 (1) 对参赛者:A到B过程,由动能定理
mgR(1-cos60°)=![]() m
m![]()
解得vB=4m/s
在B处,由牛顿第二定律
NB-mg=m ![]()
解得NB=2mg=1 200N
根据牛顿第三定律:参赛者对轨道的压力
N′B=NB=1 200N,方向竖直向下.
(2) C到D过程,由动能定理
-μ2mgL2=0-![]() m
m![]()
解得vC=6m/s
B到C过程,由牛顿第二定律μ1mg=ma
解得a=4m/s2(2分)
参赛者加速至vC历时t=![]() =0.5s
=0.5s
位移x1=![]() t=2.5m<L1
t=2.5m<L1
参赛者从B到C先匀加速后匀速,传送带顺时针运转,速率v=6m/s.
(3) 0.5s内传送带位移x2=vt=3m
参赛者与传送带的相对位移Δx=x2-x1=0.5m
传送带由于传送参赛者多消耗的电能
E=μ1mgΔx+![]() m
m![]() -
-![]() m
m![]() =720J.
=720J.

练习册系列答案
相关题目