题目内容
2.甲,乙两颗人造卫星在同一平面内沿同一方向做匀速圆周运动,甲卫星距离地面的高度是地球半径的$\frac{1}{2}$,乙卫星距离地面的高度是地球半径的5倍.某时刻两卫星相距最近,问:经过多少个乙卫星做圆周运动的周期,两卫星第一次相距最远?分析 卫星做速圆周运动,根据开普勒第三定律--周期定律可求周期之比.某时刻两卫星正好同时通过地面上同一点的正上方,当两颗卫星转动角度相差π时,相距最远.
解答 解:(1)由题甲乙两卫星的轨道分别为 r1=$\frac{3R}{2}$,r2=6R
由开普勒行星运动规律$\frac{{R}^{3}}{{T}^{2}}=k$,k相同,则得$\frac{{r}_{1}^{3}}{{T}_{1}^{2}}=\frac{{r}_{2}^{3}}{{T}_{2}^{2}}$
所以$\frac{{T}_{1}}{{T}_{2}}$=$\frac{{r}_{1}^{\frac{3}{2}}}{{r}_{2}^{\frac{3}{2}}}$=$\frac{1}{8}$
设经过t时间 二者第一次相距最远,若两卫星同向运转,此时甲比乙多转π角度,
则 $\frac{2π}{{T}_{1}}t-\frac{2π}{{T}_{2}}t=π$
这段时间乙经过的周期数为n=$\frac{t}{{T}_{2}}$
解得,n=$\frac{1}{14}$
答:经过$\frac{1}{14}$个乙卫星做圆周运动的周期,两卫星第一次相距最远.
点评 本题既可应用万有引力提供向心力求解,也可应用开普勒行星运动定律求解,以后者较为方便,两卫星何时相距最远的求解,要分同向运转与反向运转两种情形,用到的数学变换相对较多,增加了本题难度.

练习册系列答案
相关题目
12.a、b为电场中的两个点,如果把q=4.0×10-9C的负电荷从a点移到b点,克服电场力做了2.0×10-7J的功,则该电荷的电势能( )
| A. | 增加了2.0×10-7J | B. | 增加了8.0×10-7J | C. | 减少了2.0×10-7J | D. | 减少了8.0×10-7J |
13.电流会生磁场,磁也会的感应出电流.下列个器件工作时用到电磁感应现象是( )
| A. | 电视机的显像管 | B. | 磁流体发电机 | C. | 指南针 | D. | 电磁炉 |
11. 如图所示,一平行板电容器,两个极板始终接在一电池的两极上,设a、b为电容器内部离开正极板不同距离的两点.以f表示一检验电荷位于a点受到的作用力,Uab为ab两点间的电势差,U为两极板之间的电压,当增大两极板之间的距离时( )
如图所示,一平行板电容器,两个极板始终接在一电池的两极上,设a、b为电容器内部离开正极板不同距离的两点.以f表示一检验电荷位于a点受到的作用力,Uab为ab两点间的电势差,U为两极板之间的电压,当增大两极板之间的距离时( )
 如图所示,一平行板电容器,两个极板始终接在一电池的两极上,设a、b为电容器内部离开正极板不同距离的两点.以f表示一检验电荷位于a点受到的作用力,Uab为ab两点间的电势差,U为两极板之间的电压,当增大两极板之间的距离时( )
如图所示,一平行板电容器,两个极板始终接在一电池的两极上,设a、b为电容器内部离开正极板不同距离的两点.以f表示一检验电荷位于a点受到的作用力,Uab为ab两点间的电势差,U为两极板之间的电压,当增大两极板之间的距离时( )| A. | f增大、U减小 | B. | f减小、Uab减小 | C. | f不变、Uab不变 | D. | Uab减小、U不变 |
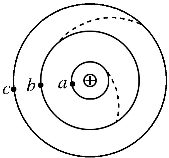 如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,则:
如图所示,a、b、c是氢原子的核外电子绕核运动的三个可能轨道,取无穷远电子的电势能为零,电子在a、b、c三个轨道时对应的电势能分别为-13.6eV、-3.4eV、-1.51eV,由于某种因素(如加热或光照)的影响,电子会沿椭圆轨道跃迁到离核更远的轨道上运动,则: 某带电物体质量为m=2kg,电量为q=6×10-3C,其与绝缘斜面间的动摩擦因数为μ=0.5,空间存在与斜面平行的匀强电场,如图所示,开始时物体置于斜面底端,释放后物体从静止开始沿斜面向上做加速运动,经过t1=0.2s后撤去电场,物体继续向上运动t2=0.4s到达运动的最高点.已知斜面倾角θ=37°.求:
某带电物体质量为m=2kg,电量为q=6×10-3C,其与绝缘斜面间的动摩擦因数为μ=0.5,空间存在与斜面平行的匀强电场,如图所示,开始时物体置于斜面底端,释放后物体从静止开始沿斜面向上做加速运动,经过t1=0.2s后撤去电场,物体继续向上运动t2=0.4s到达运动的最高点.已知斜面倾角θ=37°.求: