题目内容
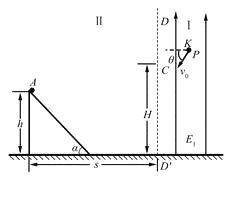
【题目】如图所示，在第一象限内有垂直纸面向里和向外的匀强磁场，磁感应强度分别为B1=0.1T、B2=0.05T，分界线OM与x轴正方向的夹角为α。在第二、三象限内存在着沿x轴正方向的匀强电场，电场强度E=1×104V/m。现有一带电粒子由x轴上A点静止释放，从O点进入匀强磁场区域。已知A点横坐标xA= -5×10-2m，带电粒子的质量m=1.6×10-24kg，电荷量q=+1.6×10-15C。
（1）要使带电粒子能始终在第一象限内运动，求α的取值范围？（用反三角函数表示）
（2）如果α=30o，则粒子能经过OM分界面上的哪些点？
（3）如果α=30o，让粒子在OA之间的某点释放，要求粒子仍能经过（2）问中的那些点，则粒子释放的位置应满足什么条件？
【答案】（1）
（2）
（k′ = 1、2、3……）（3）
（n′ = 1、2、3……）
【解析】（1）粒子进入匀强磁场后，做匀速圆周运动。设在B1中运动的半径为r1，在B2中运动的半径为r2，
由
B1= 2 B2
得 r2 = 2r1
由几何关系解得
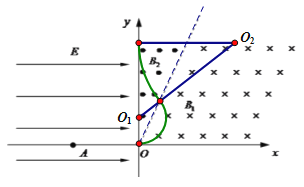
（2）当α=30o时，粒子每次在任意一个磁场中运动的圆弧的圆心角均为60o，弦长均等于半径。
粒子在电场中运动 
粒子在磁场中运动 
解得：
OM上经过的点距离O点的距离是
（k = 1、2、3……）
或 （k′ = 1、2、3……）
（3）要仍然经过原来的点，需满足 
（n = 1、2、3……）
解得
即
粒子释放的位置应满足 
（n = 1、2、3……）
或者
（n′ = 1、2、3……）
解得，
即
粒子释放的位置应满足 （n′ = 1、2、3……）
【题目】某同学用如图所示的实验装置来验证“力的平行四边形定则”。弹簧测力计A挂与固定点P，下端用细线挂一重物M。弹簧测力计B的一端用细线系于O点，手持另一端向左拉，使结点O静止在某位置。分别读出弹簧测力计A和B的示数，并在贴与竖直木板的白纸上记录O点的位置和拉线的方向。
（1）本实验用的弹簧测力计示数的单位为N，图中A的示数为 N。
（2）下列不必要的实验要求是 。（请填写选项前对应的字母）
A．应测量重物M所受的重力 |
B．弹簧测力计应在使用前校零 |
C．拉线方向应与木板平面平行 |
D．改变拉力，进行多次实验，每次都要使O点静止在同一位置 |
