题目内容
19. 如图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场.初速度为v0,带电量为q、质量为m的离子从x轴上的A点进入磁场区域,速度与x轴正向成60°角.经磁场偏转后,过y轴上的P点且垂直y轴进入电场区域,经电场偏转并击中x轴上的C点.不计重力,已知OA=d,OC=$\sqrt{2}$d.求:
如图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场.初速度为v0,带电量为q、质量为m的离子从x轴上的A点进入磁场区域,速度与x轴正向成60°角.经磁场偏转后,过y轴上的P点且垂直y轴进入电场区域,经电场偏转并击中x轴上的C点.不计重力,已知OA=d,OC=$\sqrt{2}$d.求:(1)磁感强度B的大小;
(2)粒子从A点到P点时间;
(3)电场强度E的大小.
分析 (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,求出粒子的轨道半径,然后由牛顿第二定律求出磁感应强度;
(2)根据粒子转过的圆心角与粒子做圆周运动的周期求出粒子的运动时间;
(3)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出电场强度.
解答 解: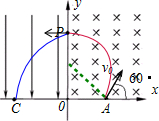 (1)粒子运动轨迹如图所示,
(1)粒子运动轨迹如图所示,
由几何知识得:r=$\frac{OA}{cos30°}$=$\frac{d}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}d}{3}$,
粒子做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qv0B=$\frac{{v}_{0}^{2}}{r}$,解得:B=$\frac{\sqrt{3}m{v}_{0}}{2qd}$;
(2)粒子在磁场中转过的圆心角:θ=120°,
粒子做圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子的运动时间:t=$\frac{θ}{360°}$T=$\frac{2πm}{3qB}$;
(3)粒子在电场中做类平抛运动,
水平方向:$\sqrt{2}$d=v0t,
竖直方向:r+rsin30°=$\frac{1}{2}$$\frac{qE}{m}$t2,
解得:E=$\frac{\sqrt{3}m{v}_{0}^{2}}{qd}$;
答:(1)磁感强度B的大小为$\frac{\sqrt{3}m{v}_{0}}{2qd}$;
(2)粒子子从A点到P点时间为$\frac{2πm}{3qB}$;
(3)电场强度E的大小为$\frac{\sqrt{3}m{v}_{0}^{2}}{qd}$.
点评 本题为带电粒子在电场、磁场中的运动类题目,若粒子垂直磁场进入,则粒子做匀速圆周运动,若垂直电场线进入电场粒子做类平抛运动.

练习册系列答案
相关题目
7.真空中保持一定距离的两个点电荷,若其中一个点电荷量增加为原来的2倍,但仍然保持它们之间的相互作用力不变,则另一点电荷的电量一定变为原来的( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{24}$ |
14.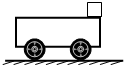 如图所示,长为L的小车置于光滑的水平面上,小车前端放一小物块,用大小为F的水平力将小车向右拉动一段距离s,物块刚好滑到小车的左端.物块与小车间的摩擦力为 f,在此过程中( )
如图所示,长为L的小车置于光滑的水平面上,小车前端放一小物块,用大小为F的水平力将小车向右拉动一段距离s,物块刚好滑到小车的左端.物块与小车间的摩擦力为 f,在此过程中( )
 如图所示,长为L的小车置于光滑的水平面上,小车前端放一小物块,用大小为F的水平力将小车向右拉动一段距离s,物块刚好滑到小车的左端.物块与小车间的摩擦力为 f,在此过程中( )
如图所示,长为L的小车置于光滑的水平面上,小车前端放一小物块,用大小为F的水平力将小车向右拉动一段距离s,物块刚好滑到小车的左端.物块与小车间的摩擦力为 f,在此过程中( )| A. | 摩擦力对小物块做的功为fs | B. | 摩擦力对系统做的总功为0 | ||
| C. | 力F对小车做的功为fL | D. | 小车克服摩擦力所做的功为fs |
11. 火箭点火后竖直上升的过程可简化为下列几个过程:
火箭点火后竖直上升的过程可简化为下列几个过程:
(1)点火后匀加速上升
(2)熄火后继续上升
(3)上升到最高点后下落.
其v-t图象如图,下列说法正确的是 ( )
 火箭点火后竖直上升的过程可简化为下列几个过程:
火箭点火后竖直上升的过程可简化为下列几个过程:(1)点火后匀加速上升
(2)熄火后继续上升
(3)上升到最高点后下落.
其v-t图象如图,下列说法正确的是 ( )
| A. | 在40秒末火箭已达到上升的最大速度 | |
| B. | 火箭达到最高点的时刻是40秒末 | |
| C. | 火箭落地的时刻是120秒末 | |
| D. | 熄火后火箭的加速度为零 |
8. 如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2.若将滑块从位置A由静止释放,当落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则这时物块的速度大小v1等于( )
如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2.若将滑块从位置A由静止释放,当落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则这时物块的速度大小v1等于( )
 如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2.若将滑块从位置A由静止释放,当落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则这时物块的速度大小v1等于( )
如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2.若将滑块从位置A由静止释放,当落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则这时物块的速度大小v1等于( )| A. | v2sinθ | B. | $\frac{{v}_{2}}{sinθ}$ | C. | v2cosθ | D. | $\frac{{v}_{2}}{cosθ}$ |
9.如图所示,物体在固定的斜面上匀速下滑,在此过程中,下列判断正确的是( )


| A. | 合力对物体做正功 | B. | 重力对物体做正功 | ||
| C. | 支持力对物体做负功 | D. | 摩擦力对物体做负功 |
 一辆汽车以15m/s的速率通过一座拱桥的桥顶时,汽车对桥面的压力等于汽车重量的一半,则这座拱桥的半径是45m,若要使汽车通过桥顶时对桥面无压力,则汽车通过桥顶时的速度大小至少是21.21m/s.(g=10m/s2)
一辆汽车以15m/s的速率通过一座拱桥的桥顶时,汽车对桥面的压力等于汽车重量的一半,则这座拱桥的半径是45m,若要使汽车通过桥顶时对桥面无压力,则汽车通过桥顶时的速度大小至少是21.21m/s.(g=10m/s2)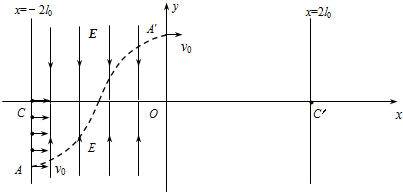 如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用.
如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用.