题目内容
10. 一辆汽车以15m/s的速率通过一座拱桥的桥顶时,汽车对桥面的压力等于汽车重量的一半,则这座拱桥的半径是45m,若要使汽车通过桥顶时对桥面无压力,则汽车通过桥顶时的速度大小至少是21.21m/s.(g=10m/s2)
一辆汽车以15m/s的速率通过一座拱桥的桥顶时,汽车对桥面的压力等于汽车重量的一半,则这座拱桥的半径是45m,若要使汽车通过桥顶时对桥面无压力,则汽车通过桥顶时的速度大小至少是21.21m/s.(g=10m/s2)
分析 在桥顶,汽车靠重力和支持力的合力提供向心力,结合牛顿第二定律求出这座拱桥的半径;当汽车对桥面的压力为零,汽车只靠重力提供向心力,根据牛顿第二定律求出汽车过桥顶时的速度大小.
解答 解:设汽车质量为m,拱桥的半径为R,桥面对汽车支持力为FN,
由牛顿第三定律可知:FN=$\frac{mg}{2}$
对汽车,由牛顿第二定律得:mg-FN=m$\frac{{v}^{2}}{R}$
所以 R=$\frac{2{v}^{2}}{g}$=2$\frac{2×1{5}^{2}}{20}$m=45m
设汽车过桥顶时对桥面恰无压力时速度为v,
对车:mg=m$\frac{{v}_{0}^{2}}{R}$
所以 v0=$\sqrt{gR}$=$\sqrt{10×45}$m/s=15$\sqrt{2}$m/s≈21.21m/s.
故答案为:45,21.21.
点评 本题是生活实际中圆周运动问题,要学会分析受力,确定向心力的来源,再运用牛顿运动定律研究.

练习册系列答案
相关题目
1. 为了节约能源,保护环境,太原市引入了一批公共自行车.这种自行车具有特殊的传动机构,它是利用杠杆凸轮联动原理制成的,其结构如图所示,小轮A和后轮B同轴固定,杠杆运动带动小轮A转动,同时使后轮B转动.已知a、b分别是小轮A和大轮B上的两点,下列说法正确的是( )
为了节约能源,保护环境,太原市引入了一批公共自行车.这种自行车具有特殊的传动机构,它是利用杠杆凸轮联动原理制成的,其结构如图所示,小轮A和后轮B同轴固定,杠杆运动带动小轮A转动,同时使后轮B转动.已知a、b分别是小轮A和大轮B上的两点,下列说法正确的是( )
 为了节约能源,保护环境,太原市引入了一批公共自行车.这种自行车具有特殊的传动机构,它是利用杠杆凸轮联动原理制成的,其结构如图所示,小轮A和后轮B同轴固定,杠杆运动带动小轮A转动,同时使后轮B转动.已知a、b分别是小轮A和大轮B上的两点,下列说法正确的是( )
为了节约能源,保护环境,太原市引入了一批公共自行车.这种自行车具有特殊的传动机构,它是利用杠杆凸轮联动原理制成的,其结构如图所示,小轮A和后轮B同轴固定,杠杆运动带动小轮A转动,同时使后轮B转动.已知a、b分别是小轮A和大轮B上的两点,下列说法正确的是( )| A. | a、b两点的线速度大小相等 | B. | a、b两点的角速度大小相等 | ||
| C. | a点的线速度比b点线速度大 | D. | a点的角速度比b点角速度大 |
18.下列哪些物理量是矢量( )
| A. | 电势 | B. | 电势差 | C. | 电势能 | D. | 磁感应强度 |
2. 如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则振动稳定后( )
如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则振动稳定后( )
 如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则振动稳定后( )
如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等.先让A摆振动起来,其他各摆随后也跟着振动起来,则振动稳定后( )| A. | 其它各摆振动振幅大小相同 | |
| B. | 其它各摆只有E摆摆动周期跟A摆相同 | |
| C. | 其它各摆振动振幅大小不相同,E摆振幅最大 | |
| D. | 其它各摆振动周期大小不同,D摆周期最大 |
20.关于电动势,下列说法正确的是( )
| A. | 电源电动势与外电路的组成有关 | |
| B. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| C. | 电源电动势的数值等于内、外电压之和 | |
| D. | 电源两极间的电压等于电源电动势 |
 在如图所示的电路中,电源电动势E=12V,内阻r=0.5Ω,R1=2Ω,R2=3Ω,滑动变阻器的总电阻R3=5Ω,试求:
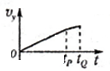
在如图所示的电路中,电源电动势E=12V,内阻r=0.5Ω,R1=2Ω,R2=3Ω,滑动变阻器的总电阻R3=5Ω,试求: 如图所示,水平抛出的物体,抵达斜面上端P处,其速度方向恰好沿斜面方向,然后紧贴斜面无摩擦滑下,以抛出点为原点,水平方向为x方向,竖直方向为y方向建立直角坐标系,下列关于物体在x、y方向运动的速度-时间图象,大致正确的是( )
如图所示,水平抛出的物体,抵达斜面上端P处,其速度方向恰好沿斜面方向,然后紧贴斜面无摩擦滑下,以抛出点为原点,水平方向为x方向,竖直方向为y方向建立直角坐标系,下列关于物体在x、y方向运动的速度-时间图象,大致正确的是( )



 如图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场.初速度为v0,带电量为q、质量为m的离子从x轴上的A点进入磁场区域,速度与x轴正向成60°角.经磁场偏转后,过y轴上的P点且垂直y轴进入电场区域,经电场偏转并击中x轴上的C点.不计重力,已知OA=d,OC=$\sqrt{2}$d.求:
如图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场.初速度为v0,带电量为q、质量为m的离子从x轴上的A点进入磁场区域,速度与x轴正向成60°角.经磁场偏转后,过y轴上的P点且垂直y轴进入电场区域,经电场偏转并击中x轴上的C点.不计重力,已知OA=d,OC=$\sqrt{2}$d.求: