题目内容
4.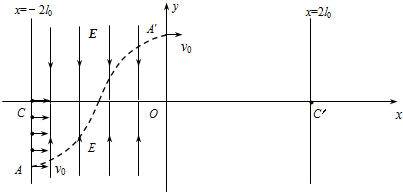 如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用.
如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用.(1)求匀强电场的电场强度E;
(2)求在AC间还有哪些位置的粒子,通过电场后也能沿x轴正方向运动?
(3)若以直线x=2l0上的某点为圆心的圆形区域内,分布着垂直于xOy平面向里的匀强磁场,使沿x轴正方向射出电场的粒子,经磁场偏转后,都能通过直线x=2l0与圆形磁场边界的一个交点处,而便于被收集,则磁场区域的最小半径是多大?相应的磁感应强度B是多大?
分析 (1)将带电粒子的运用沿水平和竖直方向正交分解,水平方向做匀速直线运动,竖直方向在x轴上下方都做匀变速直线运动,根据牛顿第二定律和运动学公式列式分析;
(2)先画出运动的一般轨迹,要使粒子通过电场后能沿x轴正方向运动,其第一次到达x轴的水平分位移的2n倍等于2l0,根据牛顿第二定律和运动学公式列式分析即可;
(3)先画出各个粒子的运动轨迹,然后根据题意确定磁场范围,最后根据洛伦兹力提供向心力求解磁感应强度.
解答 解:(1)设从A点射入的粒子由A点到A'点的运动时间为t,根据运动轨迹的对成称性有
x方向有:2L0=v0t得:t=$\frac{2{l}_{0}}{{v}_{0}}$…①
y方向有:l0=$\frac{qE}{2m}$($\frac{t}{2}$)2…②
解得:E=$\frac{2m{v}_{0}^{2}}{q{l}_{0}}$…③
即从AC间入射的粒子穿越电场区域的时间t为$\frac{2{l}_{0}}{{v}_{0}}$,匀强电场的电场强度E的大小为$\frac{2m{v}_{0}^{2}}{q{l}_{0}}$.
(2)设到C点距离为△y处射出的粒子通过电场后也沿x轴正方向,粒子第一次到达x轴用时△t,水平分位移△x,
则△x=v0△t…④
△y=$\frac{qE}{2m}$(△t)2…⑤
要粒子从电场中射出时速度方向也沿x轴正方向,必须满足条件2l0=n•2△x(n=1,2,3…)…⑥
联立③④⑤⑥解得:△y=$\frac{1}{{n}^{2}}$l0…⑦
故粒子从电场中射出时速度方向也沿x轴正方向,必须是在AC间纵坐标为:y=-$\frac{{l}_{0}}{{n}^{2}}$,(n=1,2,3…)…⑧
(3)当n=1时,粒子射出的坐标为y1=l0…⑨
当n=2时,粒子射出的坐标为y2=-$\frac{{l}_{0}}{4}$…⑩
当n≥3时,沿x轴正方向射出的粒子分布在y1到y2之间(如图所示).
y1、y2之间距离为 L=y1-y2=$\frac{5{l}_{0}}{4}$…(11)
所以,磁场圆O1的最小半径R=$\frac{l}{2}$$\frac{5{l}_{0}}{8}$…(12)
若使粒子经磁场后汇集于直线x=2l0与圆形磁场边界的一个交点,分析知此点只能是答图中的Q点,且粒子在磁场中做圆周运动的半径等于磁场区域圆半径.
由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{R}$…(13)
联立(12)(13)得:B=$\frac{8m{v}_{0}}{5q{l}_{0}}$…(14)
即磁场区域的最小半径是$\frac{5{l}_{0}}{8}$,相应的磁感应强度B是$\frac{8m{v}_{0}}{5q{l}_{0}}$.
答:(1)求匀强电场的电场强度为 $\frac{2m{v}_{0}^{2}}{q{l}_{0}^{\;}}$;
(2)y=-$\frac{{l}_{0}}{{n}^{2}}$,(n=1,2,3…)位置的粒子,通过电场后也能沿x轴正方向运动;
(3)磁场区域的最小半径是$\frac{5{l}_{0}}{8}$,相应的磁感应强度B是$\frac{8m{v}_{0}}{5q{l}_{0}}$.
点评 本题关键是将粒子的运动沿着水平方向和竖直方向正交分解,然后根据牛顿运动定律和运动学公式列式分析求解;解题过程中要画出轨迹图分析,特别是第三小题,要画出准确的圆轨迹图分析才能有助与问题的解决.

 阅读快车系列答案
阅读快车系列答案| 器材 | 规格 | 器材 | 规格 |
| 小电珠 | 标有“3.8V,0.3A”字样 | 滑动变阻器R1 | 最大阻值10Ω,额定电流1.0A |
| 电压表V | 量程0~5V,内阻5kΩ | 滑动变阻器R2 | 最大阻值1kΩ,额定电流0.5A |
| 电流表A1 | 量程0~100mA,内阻4Ω | 直流电源E | 电动势约6V,内阻约0.5Ω |
| 电流表A2 | 量程0~500mA,内阻0.4Ω | 导线、电健等 |
(2)本实验最好用以下哪个电路A.

| A. | 电梯可能向上加速运动,重物质量为1kg | |
| B. | 电梯可能向上减速运动,加速度大小为2m/s2 | |
| C. | 电梯可能向下加速运动,重物质量为0.8kg | |
| D. | 电梯可能向下减速运动,加速度大小为2m/s2 |
 A、B两个点电荷在真空中所产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )
A、B两个点电荷在真空中所产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )| A. | 这两点电荷一定是同种电荷 | B. | D、C这两点的电势相等 | ||
| C. | D、C两点电场强度相等 | D. | C点的电场强度比D点的电场强度大 |


 如图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场.初速度为v0,带电量为q、质量为m的离子从x轴上的A点进入磁场区域,速度与x轴正向成60°角.经磁场偏转后,过y轴上的P点且垂直y轴进入电场区域,经电场偏转并击中x轴上的C点.不计重力,已知OA=d,OC=$\sqrt{2}$d.求:
如图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场.初速度为v0,带电量为q、质量为m的离子从x轴上的A点进入磁场区域,速度与x轴正向成60°角.经磁场偏转后,过y轴上的P点且垂直y轴进入电场区域,经电场偏转并击中x轴上的C点.不计重力,已知OA=d,OC=$\sqrt{2}$d.求: