��Ŀ����
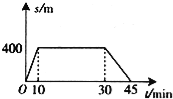
����Ŀ����ͼ��ʾ��ˮƽ���AB����ֱ��Բ�ι��������B�㣬��Բ�������ߵ�ΪC���뾶ΪR�����ʵ�����˹̶���A�㣬��AB������ã�����Ϊm��С���뱻ѹ���ĵ��ɽ����š���˩�ӡ����ͷ�С���뿪���ɺ�B�㣬����Բ�����ǡ����ͨ����ߵ�C��ˮƽ�ɳ�������ˮƽ����ϵ�D��(ͼ��δ���)���������������Ħ���������������������ٶ�Ϊg����:
(1)С��C��ʱ���ٶȴ�С
(2)B��D��������
(3)С���ͷ�ǰ���ɵĵ�������
���𰸡���1��![]() ��2��2R��3��2.5mgR
��2��2R��3��2.5mgR
��������
��1��С����C��ʱ���������ṩ����������ţ�ٵڶ����ɵã�![]()
�ɵã�vC=![]()
��2��С���뿪C�����ƽ���˶�����
��ֱ�����У�2R=![]() gt2
gt2
ˮƽ�����У�x=vCt
������ã�x=2R��
��С���һ����ص���B��ľ�����2R��
��3���ӿ�ʼ�ͷŵ��ɵ�С��C��Ĺ��̣��ɻ�е���غ㶨�ɵã�
�ͷ�С��˲�䵯�ɵĵ������ܣ�Ep=2mgR+![]() mvC2
mvC2
��ã�Ep=2.5mgR

��ϰ��ϵ�д�
�����Ŀ