题目内容
13.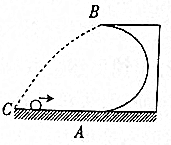 如图所示,半径R=2.5m的光滑半圆形轨道固定在水平地面上,一小球以某一速度从半圆形轨道的最低点A冲上轨道,从半圆轨道的最高点B水平飞出,小球在B点时对轨道的压力恰好等于小球受到的重力.不计空气阻力,重力加速度g=10m/s2.求:
如图所示,半径R=2.5m的光滑半圆形轨道固定在水平地面上,一小球以某一速度从半圆形轨道的最低点A冲上轨道,从半圆轨道的最高点B水平飞出,小球在B点时对轨道的压力恰好等于小球受到的重力.不计空气阻力,重力加速度g=10m/s2.求:(1)小球达到B点时的速度大小;
(2)小球从B点水平飞出到落地的过程中的位移大小.
分析 (1)小球将要从轨道口飞出时,轨道的压力恰好等于小球的重力,根据牛顿第二定律列式求解;
(2)从轨道口B处水平飞出后,小球做平抛运动,由平抛运动的规律可以求得落地过程中的位移.
解答 解:(1)当小球在B点时由向心力的公式可得:
N+mg=m$\frac{{{v}_{B}}^{2}}{R}$,
所以有:mg+mg=m$\frac{{{v}_{B}}^{2}}{R}$,
解得:vB=$\sqrt{2gR}$=$\sqrt{2×10×2.5}=5\sqrt{2}$m/s,
(2)小球从B点飞出后,做平抛运动,设运动的时间是t:
由 2R=$\frac{1}{2}$gt2
所以 t=2$\sqrt{\frac{R}{g}}$,
小球落地点到A点的距离为:x=vBt=$\sqrt{2gR}$×2$\sqrt{\frac{R}{g}}$=$2\sqrt{2}$R
小球从B点水平飞出到落地的过程中的位移大小为:s=$\sqrt{{x}^{2}+(2R)^{2}}$
代入数据得:s=$5\sqrt{3}$m
答:(1)小球达到B点时的速度大小是$5\sqrt{2}$m/s;
(2)小球从B点水平飞出到落地的过程中的位移大小是$5\sqrt{3}$m.
点评 本题是牛顿第二定律、平抛运动规律的综合运用问题,关键理清小球的运动情况,然后分阶段列式求解,难度适中.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
3.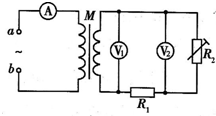 如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
 如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )| A. | 当R2所在处出现火警时,电阻R1的功率变小 | |
| B. | 当R2所在处出现火警时,电压表V2的示数变小 | |
| C. | 当R2所在处出现火警时,电流表A的示数变小 | |
| D. | 电压表V1示数为22V |
1.物体沿一条直线运动,下列说法正确的是( )
| A. | 物体在某时刻的速度为3m/s,则物体在1s内一定走3m | |
| B. | 物体在某1s内的平均速度是3m/s,则物体在这1s内的位移一定是3m | |
| C. | 物体在某段时间内的平均速度是3m/s,则物体在其中某1s内的位移一定是3m | |
| D. | 若物体做匀变速直线运动时,在发生某段位移过程中的平均速度是3m/s,则物体在这段位移的一半时的速度一定是大于3m/s |
8.物体做匀减速直线运动,最初两个2s内的位移分别10m和6m.则下列说法正确的是( )
| A. | 物体的初速度大小为6 m/s | B. | 物体的加速度大小为2m/s2 | ||
| C. | 物体第4s内的位移大小为5m | D. | 物体第4s末的速度大小为1m/s |
18.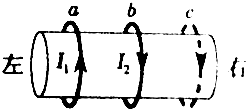 在绝缘圆柱体上a、b两位置固定有两个金属圆弧,当两环通有如图所示电流时,b处金属圆环受到的安培力为F1;若将b处金属圆环移到位置c,则通有电流为I2的金属圆环受到的安培力为F2.今保持b处金属原子位置不变,在位置c再放置一个同样的金属圆环,并通有与a处金属圆环同向、大小为I2的电流,则在a位置的金属圆环受到的安培力( )
在绝缘圆柱体上a、b两位置固定有两个金属圆弧,当两环通有如图所示电流时,b处金属圆环受到的安培力为F1;若将b处金属圆环移到位置c,则通有电流为I2的金属圆环受到的安培力为F2.今保持b处金属原子位置不变,在位置c再放置一个同样的金属圆环,并通有与a处金属圆环同向、大小为I2的电流,则在a位置的金属圆环受到的安培力( )
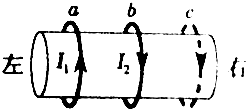 在绝缘圆柱体上a、b两位置固定有两个金属圆弧,当两环通有如图所示电流时,b处金属圆环受到的安培力为F1;若将b处金属圆环移到位置c,则通有电流为I2的金属圆环受到的安培力为F2.今保持b处金属原子位置不变,在位置c再放置一个同样的金属圆环,并通有与a处金属圆环同向、大小为I2的电流,则在a位置的金属圆环受到的安培力( )
在绝缘圆柱体上a、b两位置固定有两个金属圆弧,当两环通有如图所示电流时,b处金属圆环受到的安培力为F1;若将b处金属圆环移到位置c,则通有电流为I2的金属圆环受到的安培力为F2.今保持b处金属原子位置不变,在位置c再放置一个同样的金属圆环,并通有与a处金属圆环同向、大小为I2的电流,则在a位置的金属圆环受到的安培力( )| A. | 大小为|F1+F2|,方向向左 | B. | 大小为|F1+F2|,方向向右 | ||
| C. | 大小为|F1-F2|,方向向左 | D. | 大小为|F1-F2|,方向向右 |
2.一质点沿直线Ox方向做加速运动,它离开O点的距离x随时间变化的关系为x=4+2t3 (m),它的速度随时间变化的关系为:v=6t2( m/s).则该质点在t=2s时的瞬时速度和t=0s到t=2s间的平均速度分别为( )
| A. | 24 m/s 10 m/s | B. | 24 m/s 8 m/s | C. | 12 m/s 24 m/s | D. | 24 m/s 12 m/s |
 减速带是交叉路口上常见的一种交通设施,在某小区门口有一橡胶减速带(如图),有一警用巡逻车正以最大速度20m/s从小区门口经过,在离减速带50m时警察发现一逃犯正以10m/s的速度骑电动车匀速通过减速带,而巡逻车要匀减速到5m/s通过减速带(减速带的宽度忽略不计),然后立即以2.5m/s2的加速度继续追赶,设在整个过程中,巡逻车与逃犯均在水平直道上运动,求从警察发现逃犯到追上逃犯需要的时间.
减速带是交叉路口上常见的一种交通设施,在某小区门口有一橡胶减速带(如图),有一警用巡逻车正以最大速度20m/s从小区门口经过,在离减速带50m时警察发现一逃犯正以10m/s的速度骑电动车匀速通过减速带,而巡逻车要匀减速到5m/s通过减速带(减速带的宽度忽略不计),然后立即以2.5m/s2的加速度继续追赶,设在整个过程中,巡逻车与逃犯均在水平直道上运动,求从警察发现逃犯到追上逃犯需要的时间. 如图所示,AB、CO为互相垂直的丁字形公路,CB为一斜直小路,CB与CO成53°角,CO间距300米,一逃犯骑着电动车以43.2km/h的速度正沿AB公路逃串.当逃犯途径路口O处时,守侯在C处的警察立即以1.2m/s2的加速度启动警车,警车加速度的大小不变,警车所能达到的最大速度为108km/h,(不考虑电动车和警车转向的时间,sin53°=0.8 cos53°=0.6,计算结果保留小数点后面二位)
如图所示,AB、CO为互相垂直的丁字形公路,CB为一斜直小路,CB与CO成53°角,CO间距300米,一逃犯骑着电动车以43.2km/h的速度正沿AB公路逃串.当逃犯途径路口O处时,守侯在C处的警察立即以1.2m/s2的加速度启动警车,警车加速度的大小不变,警车所能达到的最大速度为108km/h,(不考虑电动车和警车转向的时间,sin53°=0.8 cos53°=0.6,计算结果保留小数点后面二位)