题目内容
质量m=10g的子弹,水平射入静止悬挂着的质量M=0.99kg的沙袋并留在其中,沙袋摆过α=60°角,悬绳长L=1m,不计沙袋大小.( g取10m/s2,不计空气阻力,)
(1)求:沙袋再次摆回最低位置时,悬绳对沙袋的拉力;
(2)若子弹射入沙袋时产生的内能有80%为子弹所吸收,子弹的比热c=495J/kg?℃,问子弹的温度升高多少度?
(1)求:沙袋再次摆回最低位置时,悬绳对沙袋的拉力;
(2)若子弹射入沙袋时产生的内能有80%为子弹所吸收,子弹的比热c=495J/kg?℃,问子弹的温度升高多少度?
分析:(1)沙袋与子弹在摆动的过程中机械能守恒,由机械能守恒定律可以求出沙袋摆到最低点时的速度,由牛顿第二定律可以求出绳子的拉力.
(2)子弹击中沙袋的过程中系统动量守恒,由动量守恒定律可以求出子弹击中沙袋前的速度,由能量守恒定律与热量公式可以求出子弹升高的温度.
(2)子弹击中沙袋的过程中系统动量守恒,由动量守恒定律可以求出子弹击中沙袋前的速度,由能量守恒定律与热量公式可以求出子弹升高的温度.
解答:解:(1)沙袋在摆到过程中机械能守恒,
在沙袋由最高点摆到最低点的过程中,
由机械能守恒定律可得:(M+m)gL(1-cosα)=
(M+m)v2 ①,
在最低点,由牛顿第二定律得:F-(M+m)g=(M+m)
②,
由①②解得,F=20N;
(2)子弹击中木块的过程中,系统动量守恒,
由动量守恒定律可得:mv0=(M+m)v ③,
由能量守恒定律可得:Q=
mv02-
(M+m)v2 ④,
由热量公式得:Q子弹=Qη=mc△t ⑤,
由①③④⑤解得:△t=80℃;
答:(1)沙袋再次摆回最低位置时,悬绳对沙袋的拉力为20N;
(2)子弹的温度升高了80℃.
在沙袋由最高点摆到最低点的过程中,
由机械能守恒定律可得:(M+m)gL(1-cosα)=
| 1 |
| 2 |
在最低点,由牛顿第二定律得:F-(M+m)g=(M+m)
| v2 |
| L |
由①②解得,F=20N;
(2)子弹击中木块的过程中,系统动量守恒,
由动量守恒定律可得:mv0=(M+m)v ③,
由能量守恒定律可得:Q=
| 1 |
| 2 |
| 1 |
| 2 |
由热量公式得:Q子弹=Qη=mc△t ⑤,
由①③④⑤解得:△t=80℃;
答:(1)沙袋再次摆回最低位置时,悬绳对沙袋的拉力为20N;
(2)子弹的温度升高了80℃.
点评:分析清楚物理过程,应用机械能守恒定律、动量守恒定律、能量守恒定律、热量公式即可正确解题.

练习册系列答案
相关题目
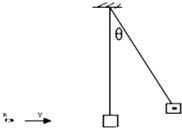 如图所示,一个冲击摆,它可以用来测量高速运动的子弹的速率.一质量m=10g的子弹,以一定水平速度射入冲击摆的木质摆锤中,冲击摆的摆锤上升至最大高度时摆线与竖直方向的夹角θ=60°.设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度g=10m/s2.求:
如图所示,一个冲击摆,它可以用来测量高速运动的子弹的速率.一质量m=10g的子弹,以一定水平速度射入冲击摆的木质摆锤中,冲击摆的摆锤上升至最大高度时摆线与竖直方向的夹角θ=60°.设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度g=10m/s2.求: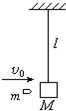 用长l=1.6m的轻绳悬挂一质量为M=1.0kg的木块(可视为质点).一颗质量m=10g的子弹以水平速度v0=500m/s沿水平方向射穿木块,射穿后的速度v=100m/s,子弹与木块的作用时间极短,如图所示.g=10m/s2.求:
用长l=1.6m的轻绳悬挂一质量为M=1.0kg的木块(可视为质点).一颗质量m=10g的子弹以水平速度v0=500m/s沿水平方向射穿木块,射穿后的速度v=100m/s,子弹与木块的作用时间极短,如图所示.g=10m/s2.求: