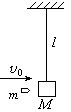题目内容
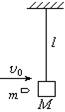
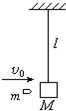 用长l=1.6m的轻绳悬挂一质量为M=1.0kg的木块(可视为质点).一颗质量m=10g的子弹以水平速度v0=500m/s沿水平方向射穿木块,射穿后的速度v=100m/s,子弹与木块的作用时间极短,如图所示.g=10m/s2.求:
用长l=1.6m的轻绳悬挂一质量为M=1.0kg的木块(可视为质点).一颗质量m=10g的子弹以水平速度v0=500m/s沿水平方向射穿木块,射穿后的速度v=100m/s,子弹与木块的作用时间极短,如图所示.g=10m/s2.求:(1)在子弹打击木块的过程中系统(子弹与木块)产生的内能Q.
(2)打击后,木块上摆的最大高度H.
(3)子弹射穿木块后的瞬间,木块所受绳的拉力T.
分析:(1)子弹穿过木块过程中,子弹与木块系统水平方向不受外力,系统动量守恒,根据动量守恒定律列式求解即可;
(2)子弹穿过木块后,木块受重力和拉力,只有重力做功,机械能守恒,根据机械能守恒定律列式求解即可;
(3)子弹穿过木块后瞬间,重力和拉力的合力提供向心力,根据牛顿第二定律和向心力公式列式求解即可.
(2)子弹穿过木块后,木块受重力和拉力,只有重力做功,机械能守恒,根据机械能守恒定律列式求解即可;
(3)子弹穿过木块后瞬间,重力和拉力的合力提供向心力,根据牛顿第二定律和向心力公式列式求解即可.
解答:解:(1)子弹穿过木块过程中,子弹与木块系统水平方向不受外力,系统动量守恒,有
mv0=mv+Mv1
解得
v1=4m/s ①
根据能量守恒定律,得到
Q=
m
-
m
-
M
=1192J ②
即在子弹打击木块的过程中系统(子弹与木块)产生的内能Q为1192J.
(2)子弹穿过木块后,木块受重力和拉力,只有重力做功,机械能守恒,有
M
=MgH ③
解得
H=
=0.8m ④
即木块上摆的最大高度H为0.8m.
(3)子弹穿过木块后瞬间,重力和拉力的合力提供向心力,根据牛顿第二定律,有
T-Mg=M
解得
T=20N ⑤
即子弹射穿木块后的瞬间,木块所受绳的拉力T为20N.
mv0=mv+Mv1
解得
v1=4m/s ①
根据能量守恒定律,得到
Q=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 |
| 1 |
| 2 |
| v | 2 1 |
即在子弹打击木块的过程中系统(子弹与木块)产生的内能Q为1192J.
(2)子弹穿过木块后,木块受重力和拉力,只有重力做功,机械能守恒,有
| 1 |
| 2 |
| v | 2 1 |
解得
H=
| ||
| 2g |
即木块上摆的最大高度H为0.8m.
(3)子弹穿过木块后瞬间,重力和拉力的合力提供向心力,根据牛顿第二定律,有
T-Mg=M
| ||
| l |
解得
T=20N ⑤
即子弹射穿木块后的瞬间,木块所受绳的拉力T为20N.
点评:本题关键是子弹射穿木块过程中,系统动量守恒,木块进行摆动过程中机械能守恒,在圆弧最低点,合力提供向心力,根据上述规律列式即可.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
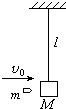 用长l=1.6m的轻绳悬挂一质量为M=1.0kg的木块.一颗质量m=10g的子弹以水平速度v0=500m/s沿水平方向射穿木块,射穿后的速度v=100m/s,如下图所示.求
用长l=1.6m的轻绳悬挂一质量为M=1.0kg的木块.一颗质量m=10g的子弹以水平速度v0=500m/s沿水平方向射穿木块,射穿后的速度v=100m/s,如下图所示.求