题目内容
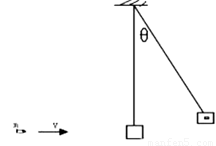
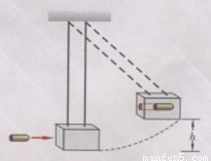
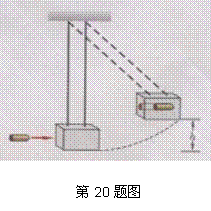
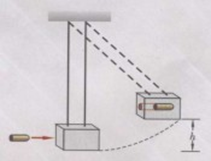
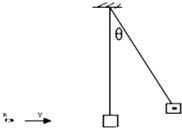 如图所示,一个冲击摆,它可以用来测量高速运动的子弹的速率.一质量m=10g的子弹,以一定水平速度射入冲击摆的木质摆锤中,冲击摆的摆锤上升至最大高度时摆线与竖直方向的夹角θ=60°.设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度g=10m/s2.求:
如图所示,一个冲击摆,它可以用来测量高速运动的子弹的速率.一质量m=10g的子弹,以一定水平速度射入冲击摆的木质摆锤中,冲击摆的摆锤上升至最大高度时摆线与竖直方向的夹角θ=60°.设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度g=10m/s2.求:(1)子弹击中摆锤后两者的共同速度是多大?
(2)子弹的初速度是多大?
分析:根据系统机械能守恒定律求出子弹击中摆锤后两者的共同的速度,再根据动量守恒定律求出子弹的初速度.
解答:解:(1)由题意,运动过程不计空气.阻力摆锤和子弹一起摆动上升的过程机械能守恒,则有:
(M+m)v共2=(m+M)gL(1-cosθ) …①
代入数据,解得:v共=3m/s …②
(2)以子弹和摆锤为系统,击打过程内力远远大于外力作用,系统在水平方向上动量守恒,则有:
mv0=(m+M)v共 …③
代入数据,解得:v0=303m/s…④
答:(1)子弹击中摆锤后两者的共同速度是3m/s.
(2)子弹的初速度是303m/s.
| 1 |
| 2 |
代入数据,解得:v共=3m/s …②
(2)以子弹和摆锤为系统,击打过程内力远远大于外力作用,系统在水平方向上动量守恒,则有:
mv0=(m+M)v共 …③
代入数据,解得:v0=303m/s…④
答:(1)子弹击中摆锤后两者的共同速度是3m/s.
(2)子弹的初速度是303m/s.
点评:本题综合考查了动量守恒定律和机械能守恒定律,难度不大,需加强这类题型的训练.

练习册系列答案
相关题目
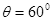 。设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度
。设摆锤质量M=1kg,摆长L=0.9m,运动过程不计空气阻力,重力加速度 。
。