题目内容
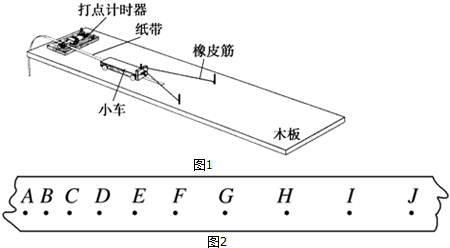
6.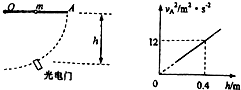 如图1所示,长直均匀光滑杆一端固定在光滑转轴O处,在水平杆的另一端A下摆经过的轨迹上安装光电门,用来测量A端的瞬时速度vA,光电门位置和转轴O的高度差可以调节,有一质量m=1kg小球套在光杆上,重力加速度为g.
如图1所示,长直均匀光滑杆一端固定在光滑转轴O处,在水平杆的另一端A下摆经过的轨迹上安装光电门,用来测量A端的瞬时速度vA,光电门位置和转轴O的高度差可以调节,有一质量m=1kg小球套在光杆上,重力加速度为g.(1)若杆的质量忽略不计,小球固定在杆的中点处,由静止释放,请写出光电门测量到的速度vA与高度差h的关系式.
(2)若杆的质量忽略不计,小球没有固定在杆上,仅套在杆上某一位置,则杆由静止释放后小球将做怎样的运动?小球下落H高度后脱离杆,则小球脱离高杆的瞬间速度多大?
(3)实际情况下杆的质量M不能忽略,拿走小球后重复实验,得到了如图2所示的vA2所示与h关系图线,g取10m/s2,证明杆绕O点转动时的动能Ek=$\frac{1}{6}$MvA2.
分析 (1)只有重力做功,机械能守恒,根据守恒定律列式求解;
(2)小球做自由落体运动,可以得到杆的末位置与水平方向成60度角,只有重力做功,机械能守恒,根据守恒定律列式求解;
(3)对杆运用动能定理列式求解即可,考虑重心位置的变化;即可证明.
解答 解:(1)由机械能守恒定律得:
$mg\frac{h}{2}=\frac{1}{2}m(\frac{{v}_{A}}{2})^{2}$
解得:${v}_{A}=2\sqrt{gh}$
(2)小球不固定时,小球将随杆下落的同时,在杆上滑动;由机械能守恒定律得:
$mgH=\frac{1}{2}m{v}^{2}$
解得脱离时小球速度为:
$v=\sqrt{2gH}$
(3)由动能定理有:
$Mg\frac{h}{2}={E}_{k}$
由图象得:h=$\frac{1}{30}$vA2
得:${E}_{K}=\frac{1}{6}M{v}_{A}^{2}$;
则可证;
答:(1)光电门测量到的速度vA与高度差h的关系式为$2\sqrt{gh}$;
(2)小球沿杆滑动;脱离瞬间杆A端速度为$\sqrt{2gH}$;
(3)可证明杆绕O点转动的动能${E}_{K}=\frac{1}{6}M{v}_{A}^{2}$;
点评 本题关键是根据动能定理多次列式后分析讨论,要注意球同时参与两个分运动,沿杆方向的分运动和随着杆一起的转动.

练习册系列答案
相关题目
5.关于静电场,下列说法正确的是( )
| A. | 沿着电场线方向,场强一定越来越小 | |
| B. | 在复杂电场中的电场线是可以相交的 | |
| C. | 同一电场线上的各点,电势一定相等 | |
| D. | 正电荷沿电场线方向移动时,电势能一定减小 |
6.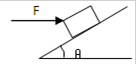 如图所示,重力为G的物体放在倾斜角为θ的光滑斜面上,一同学用水平力F作用于物体上使其静止,则斜面所受到的压力大小为( )
如图所示,重力为G的物体放在倾斜角为θ的光滑斜面上,一同学用水平力F作用于物体上使其静止,则斜面所受到的压力大小为( )
 如图所示,重力为G的物体放在倾斜角为θ的光滑斜面上,一同学用水平力F作用于物体上使其静止,则斜面所受到的压力大小为( )
如图所示,重力为G的物体放在倾斜角为θ的光滑斜面上,一同学用水平力F作用于物体上使其静止,则斜面所受到的压力大小为( )| A. | G | B. | $\frac{G}{cosθ}$ | C. | Gsinθ+Fsinθ | D. | $\sqrt{{G}^{2}+{F}^{2}}$ |
11.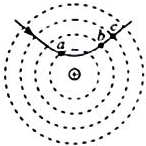 如图虚线为一组间距相等的同心圆,圆心处固定一带正电的点电荷.一带电粒子以一定初速度射入电场,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点是实线与虚线的交点.则该粒子( )
如图虚线为一组间距相等的同心圆,圆心处固定一带正电的点电荷.一带电粒子以一定初速度射入电场,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点是实线与虚线的交点.则该粒子( )
 如图虚线为一组间距相等的同心圆,圆心处固定一带正电的点电荷.一带电粒子以一定初速度射入电场,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点是实线与虚线的交点.则该粒子( )
如图虚线为一组间距相等的同心圆,圆心处固定一带正电的点电荷.一带电粒子以一定初速度射入电场,实线为粒子仅在电场力作用下的运动轨迹,a、b、c三点是实线与虚线的交点.则该粒子( )| A. | 带正电 | |
| B. | 在c点受力最大 | |
| C. | 在b点的电势能小于在c点的电势能 | |
| D. | 由a点到b点的动能变化大于由b点到c点的动能变化 |
18.关于原子结构和核反应的说法中正确的是( )


| A. | 卢瑟福在α粒子散射实验基础上提出了原子的核式结构模型 | |
| B. | 天然放射现象的发现,揭示了原子核是由质子和中子组成的 | |
| C. | 据图可知,原子核A裂变成原子核B和C要放出核能量 | |
| D. | 据图可知,原子核D和E聚变成原子核F要吸收能量 |
16.某同学利用如图所示的实验装置验证机械能守恒定律.
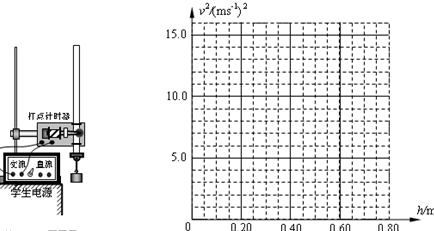
(1)下列有关实验过程的说法中正确的是AC.
A.本实验不必用停表测出重物下落的时间
B.验证时,必须测量重物的质量或重力
C.实验操作时,注意手提着纸带使重物靠近计时器,先接通计时器电源,然后松开纸带
D.如果打点计时器没有竖直放置,重物下落时,其重力势能有一部分消耗在纸带摩擦上,就会造成重力势能的变化小于动能的变化
(2)该同学正确操作得到的打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1,2,3,4,5,6,7,测量各计数点到第一个计数点的距离h,并正确求出打相应点时的速度v,各计数点对应的数据见表:
请在如图所示的坐标系中,描点作出v2-h图象;由图线可知,重物下落的加速度g=9.75m/s2(保留三位有效数字);若当地的重力加速度为9.80m/s2,根据作出的图线,能粗略验证自由下落的重物机械能守护的依据是图线为通过坐标原点的一条直线,斜率g′与g基本相等.

(1)下列有关实验过程的说法中正确的是AC.
A.本实验不必用停表测出重物下落的时间
B.验证时,必须测量重物的质量或重力
C.实验操作时,注意手提着纸带使重物靠近计时器,先接通计时器电源,然后松开纸带
D.如果打点计时器没有竖直放置,重物下落时,其重力势能有一部分消耗在纸带摩擦上,就会造成重力势能的变化小于动能的变化
(2)该同学正确操作得到的打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1,2,3,4,5,6,7,测量各计数点到第一个计数点的距离h,并正确求出打相应点时的速度v,各计数点对应的数据见表:
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| h/m | 0.124 | 0.194 | 0.279 | 0.380 | 0.497 | 0.630 | 0.777 |
| v/m•s-1 | 1.94 | 2.33 | 2.73 | 3.13 | 3.50 | ||
| v2/(m2•s-2) | 3.76 | 5.43 | 7.45 | 9.80 | 12.3 |

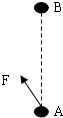 如图在纸面内有一匀强电场,一带正电的小球(不计重力)在恒力F作用下沿虚线从A点匀速运动到B点.已知力F和AB间的夹角θ,点A、B间的距离为d,小球带电q,则下列结论正确的是( )
如图在纸面内有一匀强电场,一带正电的小球(不计重力)在恒力F作用下沿虚线从A点匀速运动到B点.已知力F和AB间的夹角θ,点A、B间的距离为d,小球带电q,则下列结论正确的是( )