题目内容
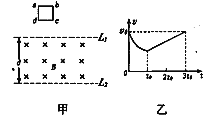
【题目】如图甲所示,光滑斜面OA与倾斜传送带AB在A点相接,且OAB在一条直线上,与水平面夹角a=37°,轻质弹赁下端固定在O点,上端可自由伸长到A点.在A点放一个物体,在力F的作用下向下缓慢压缩弹簧到C点,该过程中力F随压缩距离x的变化如图乙所示。已知物体与传送带间动牌擦因数μ=0.5,传送带AB部分长为5m,顺时针转动,速度v=4m/s,重力加速度g取l0m/s2.(sin37°=0.6,cos37°=0.8) 求:

(1)物体的质量m;
(2)弹簧从A点被压缩到C点过程中力F所做的功W;
(3)若在C点撤去力F,物体被弹回并滑上传送带,同物体在传送带上最远能到何处?
【答案】(1)5kg(2)90J(3)恰好到达传送带顶端B点
【解析】(1)由图像可知:
mg sin 370=30N……①
解得m=5kg
(2)图乙中图线与横轴所围成的面积表示力F所做的功:
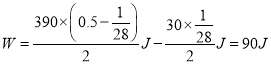 ……②.
……②.
(3)撒去力F,设物体返回至A点是速度大小为v0,
从A出发两次返回A处的过程应用动能定理:
![]() ……③
……③
箱得:v0=6m/s
由于v0>v,物块所受摩擦力沿传送带向下,设此阶段加速度大小为a1,
由牛顿第二定律:mgsin 370+μmgcos370=ma1……④
解得:a1=10m/s2
速度减为v时,设沿斜面向上发生的位移大小为x1,由运动学规律:
![]() .......⑤
.......⑤
解得:x1=1m
此后摩擦力改变方向,由于mgsin37°>μmgcos37°,所以物块所受合外力仍沿传送带向下,设此后过程加速度大小为a2,再由牛顿第二定律:
mg sin37°-μmg cos 37°=ma
设之后沿斜面向上发生的最大位移大小为x2,由运动学规律:
. ![]() ……⑦
……⑦
解得:x2=4m
所以物块能够在传送带上发生的最大位移:xm=x1+x2=5m
即恰好到达传送带顶端B点