题目内容
[物理-选修3-4]

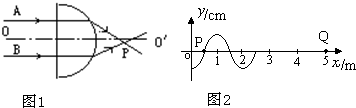
(1)如图1所示,在xOy平面内有一列沿x轴传播的简谐横波,频率为2.5HZ.在t=0时,P点位于平衡位置,且速度方向向下,Q点位于平衡位置下方的最大位移处.则在t=0.35s时,P、Q两质点
A.位移大小相等,方向相同
B.速度大小相等,方向相同
C.速度大小相等,方向相反
D.加速度大小相等,方向相反
(2)两束平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图2所示.已知其中一条光线沿直线穿过玻璃,它的入射点是O;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃截面的圆半径为R,OA=
,OP=
R.求玻璃材料的折射率.

(1)如图1所示,在xOy平面内有一列沿x轴传播的简谐横波,频率为2.5HZ.在t=0时,P点位于平衡位置,且速度方向向下,Q点位于平衡位置下方的最大位移处.则在t=0.35s时,P、Q两质点
BD
BD
A.位移大小相等,方向相同
B.速度大小相等,方向相同
C.速度大小相等,方向相反
D.加速度大小相等,方向相反
(2)两束平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图2所示.已知其中一条光线沿直线穿过玻璃,它的入射点是O;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃截面的圆半径为R,OA=
| R |
| 2 |
| 3 |
分析:(1)由频率求出波的周期,画出波形,运用波形的平移法,确定出PQ两点的位移关系.分两种方向进行分析.再判断速度、加速度的关系.
(2)作出光路图,结合折射定律和几何关系求出玻璃的折射率.
(2)作出光路图,结合折射定律和几何关系求出玻璃的折射率.
解答:(1)解:由题,频率为f=2.5Hz,则周期为T=0.4s.在t=0时,P点位于平衡位置,且速度方向向下,Q点位于平衡位置下方的最大位移处,画出波形如实线所示.
若波沿x轴正方向,在t=0.35s=
T时,波形向右平移
波长,如图虚线所示,由图看出,该时刻两质点的位移大小相等,方向相反,速度大小,方向相同;加速度大小相等,方向相反.
若波沿x轴负方向,同理得到同样的结论.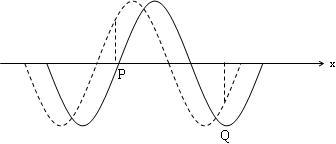
故选BD.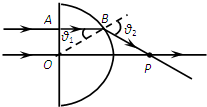
(2)作出光路如图所示,其中一条光线沿直线穿过玻璃,可知O点为圆心;
另一条光线沿直线进入玻璃,在半圆面上的入射点为B,入射角设为θ1,折射角设为θ2
则sinθ1=
=
得θ1=300
因OP=
R,由几何关系知BP=R,则折射角θ2=600
由折射定律得玻璃的折射率为n=
=
=
=1.73.
答:玻璃的折射率为1.73.
若波沿x轴正方向,在t=0.35s=
| 7 |
| 8 |
| 7 |
| 8 |
若波沿x轴负方向,同理得到同样的结论.

故选BD.

(2)作出光路如图所示,其中一条光线沿直线穿过玻璃,可知O点为圆心;
另一条光线沿直线进入玻璃,在半圆面上的入射点为B,入射角设为θ1,折射角设为θ2
则sinθ1=
| OA |
| OB |
| 1 |
| 2 |
得θ1=300
因OP=
| 3 |
由折射定律得玻璃的折射率为n=
| sinθ2 |
| sinθ1 |
| sin60° |
| sin30° |
| 3 |
答:玻璃的折射率为1.73.
点评:解决本题的关键掌握波动与振动的关系,以及掌握折射定律.光学题目对几何能力要求较高,要加强训练.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 【物理-选修3-4】
【物理-选修3-4】

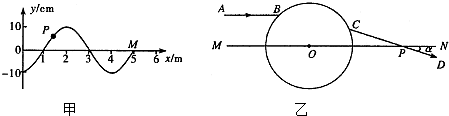
 【物理--选修3-4】
【物理--选修3-4】