题目内容
[物理--选修3-4]
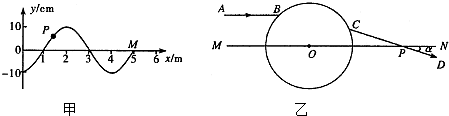
(1)一列简谐横波沿x轴正向传播;从波传到x=1.5m的P点时开始计时,此时P点从平衡位置开始沿y轴正方向振动.在t=1.1s时,PM间第一次形成图示波形,此时x=5m的M点正好在平衡位置,如图所示.下列说法正确的是 .
A.这列波的传播周期是0.8s
B.这列波的传播速度是5m/s
C.图中P点振动方向沿y轴正方向
D.图中P点的位移是y=5
cm
E.再过1.0s,质元M点向沿x轴正向迁移5m
(2)如图所示,MN是一条通过透明球体球心的直线,在真空中波长为λ0=564nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的
倍,且与MN所成的夹角α=30°.求:
①透明体的折射率n;
②此单色光在透明球体中的波长λ.
(1)一列简谐横波沿x轴正向传播;从波传到x=1.5m的P点时开始计时,此时P点从平衡位置开始沿y轴正方向振动.在t=1.1s时,PM间第一次形成图示波形,此时x=5m的M点正好在平衡位置,如图所示.下列说法正确的是
A.这列波的传播周期是0.8s
B.这列波的传播速度是5m/s
C.图中P点振动方向沿y轴正方向
D.图中P点的位移是y=5
| 2 |
E.再过1.0s,质元M点向沿x轴正向迁移5m
(2)如图所示,MN是一条通过透明球体球心的直线,在真空中波长为λ0=564nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的
| 2 |
①透明体的折射率n;
②此单色光在透明球体中的波长λ.

分析:(1)简谐横波沿x轴正向传播,起振点是从开始沿y轴正方向振动,走在最前面的是包含波峰的一个段,M点是正从平衡位置开始沿y轴负方向振动,M点不是波前,波前是在M点前面半个波长处,即x=7m处,P点到波前的距离为5.5m,即
个波长,时间上相差
个周期,为1.1s,即
T=1.1s,可知P点的周期.读出波长,由v=
求出波速v.P点开始振动的方向与图示时刻x=5m处质点的振动方向相同.根据PM间的距离判断M点开始振动时,P点的位置.
(2)连接OB、BC,在B点光线的入射角、折射角分别标为i、r,作出光路图,根据几何关系求出入射角与折射角,根据折射定律求解折射率,根据波速、波长、频率的关系即可求得此单色光在透明球体中的波长.
| 11 |
| 8 |
| 11 |
| 8 |
| 11 |
| 8 |
| λ |
| T |
(2)连接OB、BC,在B点光线的入射角、折射角分别标为i、r,作出光路图,根据几何关系求出入射角与折射角,根据折射定律求解折射率,根据波速、波长、频率的关系即可求得此单色光在透明球体中的波长.
解答:解:(1)A、由图看出,波长为λ=4m.
起振点是从开始沿y轴正方向振动,所以走在最前面的是包含波峰的一个段,M点是正从平衡位置开始沿y轴负方向振动,M点不是波前,波前是在M点前面半个波长处,即x=7m处,P点到波前的距离为5.5m,即
个波长,时间上相差
个周期,为1.1s,即
T=1.1s,所以周期T=0.8s,故A正确.
B、由波速公式v=
得,该波的波速为:v=
=
=5m/s,故B正确.
C,根据波形的平移法可知,P点振动方向沿y轴负方向运动.故C错误.
D、根据数学知识可知,若以角度为横坐标,正弦函数的周期为2π,对于1-5m这段图线来看,x=1.5m相当于
,则P的点纵坐标y=10sin
cm=5
cm,故D正确.
E、M点只在自己平衡位置上下振动,不随波向前平移,故E错误.
故答案为:ABD
(2)连接OB、BC,在B点光线的入射角、折射角分别标为i、r,如图所示.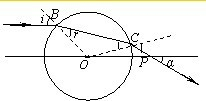
在△OCP中:有
=
由题有:OP=
OC,α=30°代入解得:∠OCP=135°(45°值舍去)
进而可得:∠COP=15°
光线从B点射入,由折射定律:n=
光线从C点射出,由折射定律:n=
,
又∠BCO=r
所以,i=45°
又:∠BCO=180°-i-∠COP=120°
故:r=30°
因此,透明体的折射率
n=
=
=
因为n=
=
=
解得:λ=
=
nm=399nm
答:
①透明体的折射率n为
;
②此单色光在透明球体中的波长λ为399nm.
起振点是从开始沿y轴正方向振动,所以走在最前面的是包含波峰的一个段,M点是正从平衡位置开始沿y轴负方向振动,M点不是波前,波前是在M点前面半个波长处,即x=7m处,P点到波前的距离为5.5m,即
| 11 |
| 8 |
| 11 |
| 8 |
| 11 |
| 8 |
B、由波速公式v=
| λ |
| T |
| λ |
| T |
| 4 |
| 0.8 |
C,根据波形的平移法可知,P点振动方向沿y轴负方向运动.故C错误.
D、根据数学知识可知,若以角度为横坐标,正弦函数的周期为2π,对于1-5m这段图线来看,x=1.5m相当于
| π |
| 4 |
| π |
| 4 |
| 2 |
E、M点只在自己平衡位置上下振动,不随波向前平移,故E错误.
故答案为:ABD
(2)连接OB、BC,在B点光线的入射角、折射角分别标为i、r,如图所示.

在△OCP中:有
| OC |
| sinα |
| OP |
| sin∠OCP |
由题有:OP=
| 2 |
进而可得:∠COP=15°
光线从B点射入,由折射定律:n=
| sini |
| sinr |
光线从C点射出,由折射定律:n=
| sin(180°-135°) |
| sin∠BCO |
又∠BCO=r
所以,i=45°
又:∠BCO=180°-i-∠COP=120°
故:r=30°
因此,透明体的折射率
n=
| sini |
| sinr |
| sin45° |
| sin30° |
| 2 |
因为n=
| c |
| v |
| c |
| f |
| λ0 |
| λ |
解得:λ=
| λ0 |
| n |
| 564 | ||
|
答:
①透明体的折射率n为
| 2 |
②此单色光在透明球体中的波长λ为399nm.
点评:第1题关键波形的平移法判断时间与周期的关系,由数学知识求P的坐标.
本题是较为复杂的几何光学问题,其基础是作出光路图,根据几何知识确定入射角与折射角,根据折射定律求解,折射过程中频率不变.
本题是较为复杂的几何光学问题,其基础是作出光路图,根据几何知识确定入射角与折射角,根据折射定律求解,折射过程中频率不变.

练习册系列答案
相关题目
 【物理-选修3-4】
【物理-选修3-4】

 【物理--选修3-4】
【物理--选修3-4】