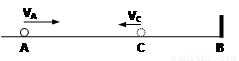题目内容
 如图,一可视为质点的小球在光滑的水平面上向右做匀速直线运动,过A点时测得速率为VA=5m/s,经过2s触及墙B,与墙B发生碰撞,碰撞时间为0.2s,然后离开墙B向左做匀速直线运动,再经过1.8s,到达距离B为3.6的C处.求:
如图,一可视为质点的小球在光滑的水平面上向右做匀速直线运动,过A点时测得速率为VA=5m/s,经过2s触及墙B,与墙B发生碰撞,碰撞时间为0.2s,然后离开墙B向左做匀速直线运动,再经过1.8s,到达距离B为3.6的C处.求:(1)AB之间的距离
(2)从A到与墙碰后返回到C的整个过程的平均速度的大小
(3)小球碰墙过程的加速度的大小和方向.
分析:根据匀速直线运动的位移公式求出AB间的距离.平均速度的大小等于位移的大小与时间的比值,求出位移和时间,从而得出平均速度的大小.根据加速度的定义式求出小球碰墙过程中的加速度大小和方向.
解答:解:(1)A到B做匀速直线运动,则AB间的距离xAB=vAt=5×2m=10m.
(2)从A到与墙碰后返回到C的整个过程的位移x=xAB-xBC=10-3.6m=6.4m.
则平均速度
=
=
=
m/s=1.6m/s.
(3)小球反弹的速度大小为vB=
=
m/s=2m/s.
规定初速度的方向为正方向,根据加速度的定义式知,a=
=
m/s2=-35m/s2
方向水平向左.
答:(1)AB之间的距离为10m.
(2)从A到与墙碰后返回到C的整个过程的平均速度的大小为1.6m/s.
(3)小球碰墙过程的加速度的大小为35m/s2,方向水平向左.
(2)从A到与墙碰后返回到C的整个过程的位移x=xAB-xBC=10-3.6m=6.4m.
则平均速度
. |
| v |
| x |
| t |
| x |
| tAC+△t+tBC |
| 6.4 |
| 2+0.2+1.8 |
(3)小球反弹的速度大小为vB=
| xBC |
| tBC |
| 3.6 |
| 1.8 |
规定初速度的方向为正方向,根据加速度的定义式知,a=
| vB-vA |
| △t |
| -2-5 |
| 0.2 |
方向水平向左.
答:(1)AB之间的距离为10m.
(2)从A到与墙碰后返回到C的整个过程的平均速度的大小为1.6m/s.
(3)小球碰墙过程的加速度的大小为35m/s2,方向水平向左.
点评:解决本题的关键掌握匀速直线运动的位移公式以及加速度的定义式,注意加速度的矢量性.

练习册系列答案
相关题目
 如图所示,ABC和DEF是在同一竖直平面内的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合.现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放,g取10m/s2.以下说法正确的是( )
如图所示,ABC和DEF是在同一竖直平面内的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合.现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放,g取10m/s2.以下说法正确的是( )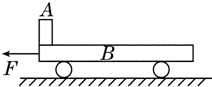 如图所示,在光滑的水平面上停放着小车B,车上左端有一可视为质点的小物块A,A和B之间的接触面前一段光滑,后一段粗糙,且后一段的动摩擦因数μ=0.4,小车长L=2m,A的质量 mA=1kg,B的质量mA=4kg,现用12N的水平力F向左拉动小车,当A到达B的最右端时,两者速度恰好相等,求:
如图所示,在光滑的水平面上停放着小车B,车上左端有一可视为质点的小物块A,A和B之间的接触面前一段光滑,后一段粗糙,且后一段的动摩擦因数μ=0.4,小车长L=2m,A的质量 mA=1kg,B的质量mA=4kg,现用12N的水平力F向左拉动小车,当A到达B的最右端时,两者速度恰好相等,求: