题目内容
19. 如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:
如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v.水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,CB为其竖直直径,(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)求:(1)小球经过C点的速度大小;
(2)小球运动到轨道最低点B时小球对轨道的压力大小;
(3)平台末端O点到A点的竖直高度H.
分析 (1)小球恰好通过最高点C,由重力提供向心力,根据牛顿第二定律求解小球经过C点的速度大小.
(2)从B点到C点,由机械能守恒定律求解B点速度.由牛顿第二定律、第三定律求得小球对轨道的压力大小.
(3)从A到B由机械能守恒定律求出A点速度,在A点进行速度的分解,根据平抛运动规律求出末端O点到A点的竖直高度H.
解答 解:(1)恰好运动到C点,有重力提供向心力,即 $mg=m\frac{v^2}{R}$
得 ${v_c}=\sqrt{gR}=5m/s$
(2)从B点到C点,由机械能守恒定律有
$\frac{1}{2}m{v_c}^2+2mgR=\frac{1}{2}m{v_B}^2$
在B点对小球进行受力分析,由牛顿第二定律有 FN-mg=m$\frac{{v}_{B}^{2}}{R}$
联立得 FN=6mg=6.0N
根据牛顿第三定律,小球对轨道的压力大小为6.0N
(3)从A到B由机械能守恒定律有
$\frac{1}{2}$mvA2+mgR(1-cos53°)=$\frac{1}{2}$mvB2
所以:${v_A}=\sqrt{105}m/s$
在A点进行速度的分解有:vy=vAsin53°
所以:$H=\frac{{{v_y}^2}}{2g}=3.36m$
答:
(1)小球经过C点的速度大小是5m/s;
(2)小球运动到轨道最低点B时小球对轨道的压力大小是6N;
(3)平台末端O点到A点的竖直高度是3.36m.
点评 本题是平抛运动和圆周运动相结合的典型题目,除了运用平抛运动和圆周运动的基本公式外,求速度的问题,机械能守恒定律或动能定理不失为一种好的方法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.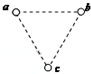 如图,在光滑绝缘水平面上,三个带电质点a、b和c分别位于边长为L的正三角形的三个顶点上;a、b电荷量均为q且为同种电荷,整个系统置于水平方向的匀强电场中.已知静电力常量为k,若三个质点均处于静止状态,则下列说法正确的是( )
如图,在光滑绝缘水平面上,三个带电质点a、b和c分别位于边长为L的正三角形的三个顶点上;a、b电荷量均为q且为同种电荷,整个系统置于水平方向的匀强电场中.已知静电力常量为k,若三个质点均处于静止状态,则下列说法正确的是( )
 如图,在光滑绝缘水平面上,三个带电质点a、b和c分别位于边长为L的正三角形的三个顶点上;a、b电荷量均为q且为同种电荷,整个系统置于水平方向的匀强电场中.已知静电力常量为k,若三个质点均处于静止状态,则下列说法正确的是( )
如图,在光滑绝缘水平面上,三个带电质点a、b和c分别位于边长为L的正三角形的三个顶点上;a、b电荷量均为q且为同种电荷,整个系统置于水平方向的匀强电场中.已知静电力常量为k,若三个质点均处于静止状态,则下列说法正确的是( )| A. | 如果a、b带正电,那么c一定带负电 | B. | 匀强电场场强的大小为$\frac{\sqrt{3}kq}{{l}^{2}}$ | ||
| C. | 质点c的电量大小为$\sqrt{2}$q | D. | 匀强电场的方向与ab边垂直背离c |
14.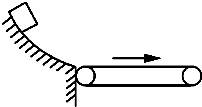 如图所示,物体沿弧形轨道滑下后进入水平传送带,传送带以图示方向匀速运转,则物体经过传送带过程中,传送带对物体所做的总功( )
如图所示,物体沿弧形轨道滑下后进入水平传送带,传送带以图示方向匀速运转,则物体经过传送带过程中,传送带对物体所做的总功( )
 如图所示,物体沿弧形轨道滑下后进入水平传送带,传送带以图示方向匀速运转,则物体经过传送带过程中,传送带对物体所做的总功( )
如图所示,物体沿弧形轨道滑下后进入水平传送带,传送带以图示方向匀速运转,则物体经过传送带过程中,传送带对物体所做的总功( )| A. | 可能为零 | B. | 一定为正功 | C. | 一定为负功 | D. | 可能为负功 |
4. 如图所示,一个带负电荷的小球在真空中水平抛出,水平方向的匀强磁场与小球的轨迹平面垂直,若小球能够落地,则( )
如图所示,一个带负电荷的小球在真空中水平抛出,水平方向的匀强磁场与小球的轨迹平面垂直,若小球能够落地,则( )
 如图所示,一个带负电荷的小球在真空中水平抛出,水平方向的匀强磁场与小球的轨迹平面垂直,若小球能够落地,则( )
如图所示,一个带负电荷的小球在真空中水平抛出,水平方向的匀强磁场与小球的轨迹平面垂直,若小球能够落地,则( )| A. | 落地时,速度方向可能竖直向下 | B. | 小球水平方向动量守恒 | ||
| C. | 小球在运动过程中机械能守恒 | D. | 小球动量的大小保持不变 |
11. 假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )
假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )
 假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )
假设月球半径为R,月球表面的重力加速度为g0,如图所示,飞船首先沿距月球表面高度为3R的圆轨道I运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ(轨道半径可近似当做R)绕月球做圆周运动.下列判断正确的是( )| A. | 飞船在轨道 I上的运行速率为$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在轨道Ⅲ绕月球运动一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ | |
| C. | 飞船在Ⅱ轨道A点速率大于在Ⅰ轨道A点速率 | |
| D. | 飞船在Ⅱ轨道B点加速度大于Ⅲ轨道B点加速度 |
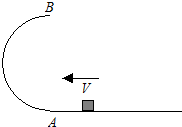 在竖直平面内有一半径为R的光滑半圆形固定轨道,其最低点A和水平面相切.一质量为m的物块从最低点以某一速度冲上轨道,到达最高点B时和半圆轨道之间的作用力的大小为mg,求:
在竖直平面内有一半径为R的光滑半圆形固定轨道,其最低点A和水平面相切.一质量为m的物块从最低点以某一速度冲上轨道,到达最高点B时和半圆轨道之间的作用力的大小为mg,求:
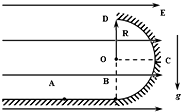 如图,ABCD为表示竖立放在场强为E=104V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与圆环相切,A为水平轨道的一点,而且AB=R=0.2m把一质量m=0.1kg、带电q=10-4C的小球,放在水平轨道的A点上面由静止开始被释放后,在轨道的内侧运动.(g取10m/s2)求:
如图,ABCD为表示竖立放在场强为E=104V/m的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与圆环相切,A为水平轨道的一点,而且AB=R=0.2m把一质量m=0.1kg、带电q=10-4C的小球,放在水平轨道的A点上面由静止开始被释放后,在轨道的内侧运动.(g取10m/s2)求: