题目内容
12．某娱乐项目中，要求参与者抛出一小球去撞击触发器成功，从而才能进入下一关．现在将这个娱乐项目简化为如下的理想模型：不计空气的阻力，假设参与者从触发器的正下方以v的速率竖直上抛一小球，小球恰好击中触发器．若参与者仍在刚才的抛出点，沿A、B、C、D四个不同的光滑轨道分别以相同的速率v抛出小球，如图所示A为半圆轨道，B为一段光滑斜面，C为一段不足$\frac{1}{4}$的圆弧轨道，D为内壁光滑的半圆轨道．则小球能够击中触发器的是（ ）
| A． | A | B． | B | C． | C | D． | D |
分析 小球在运动的过程中机械能守恒，根据机械能守恒定律，以及到达最高点的速度能否为零，判断小球进入右侧轨道能否到达h高度．
解答 解：由题意，小球以v竖直上抛的最大高度为h，说明到达最大高度时速度为0．根据机械能守恒有：mgh=$\frac{1}{2}m{v}^{2}$ ①
A、根据圆周运动知识可知，小球要到达触发器速度不为0，由机械能守恒得：$\frac{1}{2}m{v}^{2}$=mgh′+$\frac{1}{2}mv{′}^{2}$ ②，由①②比较知，h′＜h，则小球上升的最大高度减小了，不能击中触发器，故A错误；
B、小球离开斜面后做斜抛运动了，到最高点时水平方向有一定的速度，最大高度小于h，不能击中触发器，故B错误；
C、根据机械能守恒定律可知，小球上升到最高点时速度刚好等于零，可以击中触发器，故C正确；
D在双轨中做圆周运动时到达最高点的速度可以为零，根据机械能守恒守恒知，小球可以上升到最高点并击中触发器，故D正确．
故选：CD．
点评 解决本题的关键掌握机械能守恒定律，以及会判断小球在最高点的速度是否为零，要明确内壁光滑的圆轨道，小球到达最高点的最小速度为$\sqrt{gr}$．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．
如图所示，A、B是一对平行的金属板，在两板间加有一周期为T的交变电压u，A板的电势φA=0，B板的电势φB随时间的变化规律为：在0到$\frac{T}{2}$的时间内，φB=φ0（φ0为正的常数）；在$\frac{T}{2}$到T的时间内，φB=-φ0；在T到$\frac{3T}{2}$的时间内，φB=φ0；在$\frac{3T}{2}$到2T的时间内，φB=-φ0…，现有一电子在t时刻从A极板附近由静止释放，不计重力，则下列判断错误的是（ ）
如图所示，A、B是一对平行的金属板，在两板间加有一周期为T的交变电压u，A板的电势φA=0，B板的电势φB随时间的变化规律为：在0到$\frac{T}{2}$的时间内，φB=φ0（φ0为正的常数）；在$\frac{T}{2}$到T的时间内，φB=-φ0；在T到$\frac{3T}{2}$的时间内，φB=φ0；在$\frac{3T}{2}$到2T的时间内，φB=-φ0…，现有一电子在t时刻从A极板附近由静止释放，不计重力，则下列判断错误的是（ ）| A． | 若t=0，则电子将一直向B板运动，最后打在B板上 | |
| B． | 若t=$\frac{3T}{8}$，则电子一定会打在B板上 | |
| C． | 若t=$\frac{T}{8}$，则电子一定会打在B板上 | |
| D． | 若t=$\frac{T}{4}$，则电子可能在A、B两极板间往复运动 |
如图所示，将一质量为m=0.1kg的小球自水平平台右端O点以初速度v．水平抛出，小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC，并沿轨道恰好通过最高点C，圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧，CB为其竖直直径，（sin53°=0.8 cos53°=0.6，重力加速度g取10m/s2）求：
如图所示，车间内的天车（有的地区交行车）将一重104N的物体沿着与水平方向成30°角的方向匀速吊起，使物体向斜上方移动了x1=6m，求：
7．如图甲所示为用拉力传感器和速度传感器“探究加速度与物体受力的关系”实验装置．用拉力传感器记录小车受到的拉力大小，在长木板上的A、B两点各安装一个速度传感器，分别记录小车到达A、B时的速率，A、B相距L=48.0cm．
（1）实验主要步骤如下：
①将拉力传感器固定在小车上；
②平衡摩擦力，让小车在没有拉力作用时能做匀速直线运动；
③把细线的一端固定在拉力传感器上，另一端通过定滑轮与钩码相连；
④接通电源后自C点释放小车，小车在细线拉动下运动，记录细线拉力F的大小及小车分别到达A、B时的速率vA、vB
⑤改变所挂钩码的数量，重复④的操作．
（2）表中记录了实验测得的几组数据，vB2-vA2是两个速度传感器记录速率的平方差，则加速度的表达式a=$\frac{{{v}_{B}^{2}-v}_{A}^{2}}{2L}$（用题中已知的符号表示），请将表中第3次的实验数据填写完整（结果保留三位有效数字）；
（3）由实验数据，得出a-F关系图线和理论图线如图乙，对比两图线，造成上述偏差的原因是没有平衡摩擦力或平衡摩擦力不足．
（1）实验主要步骤如下：
①将拉力传感器固定在小车上；
②平衡摩擦力，让小车在没有拉力作用时能做匀速直线运动；
③把细线的一端固定在拉力传感器上，另一端通过定滑轮与钩码相连；
④接通电源后自C点释放小车，小车在细线拉动下运动，记录细线拉力F的大小及小车分别到达A、B时的速率vA、vB
⑤改变所挂钩码的数量，重复④的操作．
（2）表中记录了实验测得的几组数据，vB2-vA2是两个速度传感器记录速率的平方差，则加速度的表达式a=$\frac{{{v}_{B}^{2}-v}_{A}^{2}}{2L}$（用题中已知的符号表示），请将表中第3次的实验数据填写完整（结果保留三位有效数字）；
| 次数 | F（N） | vB2-vA2（m2/s2） | a（m/s2） |
| 1 | 0.60 | 0.77 | 0.80 |
| 2 | 1.04 | 1.61 | 1.68 |
| 3 | 1.42 | 2.34 | |
| 4 | 2.62 | 4.65 | 4.84 |
| 5 | 3.00 | 5.49 | 5.72 |
如图所示，质量为m1的物体甲通过三段轻绳悬挂，三段轻绳的结点为O．轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连，轻绳OA与竖直方向的夹角θ=37°，物体甲、乙均处于静止状态．（取g=10m/s2，sin37°=0.6，cos37°=0.8，设最大静摩擦力等于滑动摩擦力）求：
1．以下是有关近代物理内容的若干叙述，其中正确的是（ ）
| A． | 原子核发生一次β衰变，该原子外层就失去一个电子 | |
| B． | 按照玻尔理论，氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时，电子的动能减小，但原子的能量增大 | |
| C． | 一束光照射到某种金属上不能发生光电效应，可能是因为这束光的光强太小 | |
| D． | 比结合能越大，原子核中核子结合得越牢固，原子核越稳定 | |
| E． | 太阳辐射的能量主要来自太阳内部的聚变反应 |
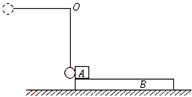质量为mB=6kg的木板B静止于光滑水平面上，物块A质量为mA=1kg，停在B的左端．质量为m=1kg的小球用长为l=0.8m的轻绳悬挂在固定点O上，将轻绳拉直至水平位置后，由静止释放小球，小球在最低点与A发生碰撞，碰撞时间极短，且无机械能损失．物块与小球可视为质点，不计空气阻力．已知A、B间的动摩擦因数μ=0.1，A离开B时的速度是B的2倍，g取10m/s2．求木板的长度d？