题目内容
如图所示,将直径为2R的半圆形导轨固定在竖直面内的A、B两点,直径AB与竖直方向的夹角为60°。在导轨上套一质量为m的小圆环,原长为2R、劲度系数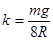 的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求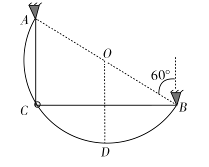
(1)圆环的速率v;
(2)导轨对圆环的作用力F的大小?
(1)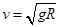 (2)
(2)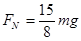
解析试题分析: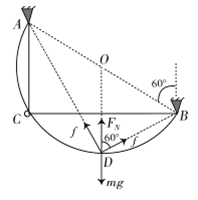
(1)由几何知识得,圆环在C点、D点时,弹性绳形变量相同,弹性势能相等。由机械能守恒定律,有 3分
3分
由几何关系可知 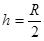 2分
2分
解得 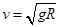 3分
3分
(2)圆环在D点受力如图,弹性绳的弹力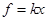 1分
1分
其中 1分
1分
由牛顿第二定律,有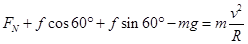 2分
2分
解得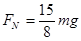 2分
2分
考点:本题考查牛顿定律和功能关系

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
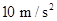 ,则物体在t=0至t=12 s这段时间的位移大小为( )
,则物体在t=0至t=12 s这段时间的位移大小为( )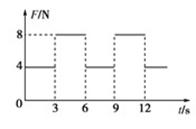

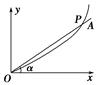
 =
= ,绳长l=2m,绳的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。(取重力加速度
,绳长l=2m,绳的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。(取重力加速度 ,
, ,
, )
)
 ,平均阻力
,平均阻力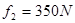 ,求选手落入水中的深度
,求选手落入水中的深度 。
。 N/C的匀强电场中,甲的质量为
N/C的匀强电场中,甲的质量为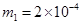 kg,带电荷量为
kg,带电荷量为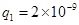 C,乙的质量为
C,乙的质量为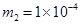 kg,带电荷量为
kg,带电荷量为 C。开始时细绳处于拉直状态。由静止释放两滑块,t=3s时细绳断裂,不计滑块间的库仑力。试求:
C。开始时细绳处于拉直状态。由静止释放两滑块,t=3s时细绳断裂,不计滑块间的库仑力。试求: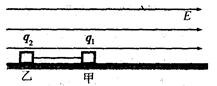

 ,为使小车恰好能通过圆形轨道的最高点D,则它在P点沿斜面向下的初速度v0。
,为使小车恰好能通过圆形轨道的最高点D,则它在P点沿斜面向下的初速度v0。