题目内容
如图所示,轨道ABO在同一竖直平面内,由光滑水平轨道OB和倾角θ=30°、高度h=1m的倾斜轨道BA连接而成, OB与BA连接处是半径很小的圆弧,水平轨道上一轻质弹簧左端O固定在竖直的墙上,质量m=0.5kg的小物块从BA轨道上A点由静止开始下滑。已知物块与倾斜轨道间的动摩擦因数 ,重力加速度g=10m/s2,弹簧形变始终在弹性限度内.求:
,重力加速度g=10m/s2,弹簧形变始终在弹性限度内.求:

(1)物块第一次在水平轨道上压缩弹簧运动到速度为零时,弹簧具有的弹性势能EP;
(2)物块在倾斜轨道上滑动的总路程s;
(3)物块第n次压缩弹簧后,沿倾斜轨道上升的最大高度hn.
 ,重力加速度g=10m/s2,弹簧形变始终在弹性限度内.求:
,重力加速度g=10m/s2,弹簧形变始终在弹性限度内.求:
(1)物块第一次在水平轨道上压缩弹簧运动到速度为零时,弹簧具有的弹性势能EP;
(2)物块在倾斜轨道上滑动的总路程s;
(3)物块第n次压缩弹簧后,沿倾斜轨道上升的最大高度hn.
(1)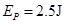 (2)
(2)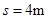 (3)
(3)
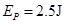 (2)
(2)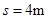 (3)
(3)
试题分析:(1)物块从A点到第一次压缩弹簧速度为零过程,
由功能关系有:
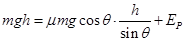 (1分)
(1分)解得:
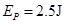 (1分)
(1分)(2)物块最终静止在水平轨道上,且弹簧形变量为零
由动能定理有:
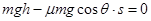 (2分)
(2分)解得:
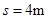 (1分)
(1分)(3)设物块第1、2、3……次压缩弹簧后,沿倾斜轨道上升的最大高度分别为h1、h2、h3……,则:
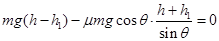
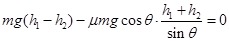
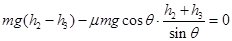 (1分)
(1分)…………
解得:
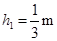 、
、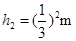 、
、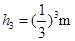 ……(1分)
……(1分)则有:
 (1分)
(1分)点评:本题难度中等,处理此题时,应利用能量守恒或能量转化角度分析问题,注意重力做功与路径无关,摩擦力做功与路径有关

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 的加速度由静止竖直下落到地面,下列说法中正确的是( )
的加速度由静止竖直下落到地面,下列说法中正确的是( )

 ,篮筐距地面高度为
,篮筐距地面高度为 ,球的质量为
,球的质量为 ,空气阻力不计,则篮球进筐时的动能为( )
,空气阻力不计,则篮球进筐时的动能为( )

 -W
-W

