题目内容
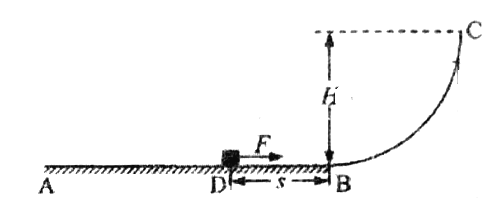
【题目】如图，AB为足够长的粗糙水平轨道，D为AB上的一点，DB长度s=2m，BC为光滑圆弧轨道，两轨道在B点平滑连接。C点高度H=4m，质量m=lkg的滑块，在水平向右的恒力F=10N作用下，从D点由静止开始运动，受到恒定的摩檫力f=6N。当滑块运动到B点后撤去恒力F。 求：（g取10m/s2）
(1)滑块从D点运动到B点的过程中合力做的功。
(2)滑块运动到B点时恒力F的功率。
(3)滑块在圆弧轨道BC上所能达到的最大高度h.
(4)若只改变出发点D的位置，其他条件不变，通过计算分析滑块能到达C点时s所满足的条件。
【答案】(1)8J；(2)40W；(3)0.8m；(4)s10m
【解析】
(1)以滑块为研究对象，DB过程中重力和支持力不做功，F做正功，摩擦力做负功，故合力做的功：
(2)设滑块运动到D点时，速度为v，根据动能定理
解得：
恒力F的功率：
(3)以滑块从D到最高点为研究过程，由动能定理得：
所以：
；
(4)以滑块从D到C点为研究过程，由动能定理得：
应满足：
s10m
练习册系列答案
相关题目
