��Ŀ����
8��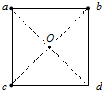 �⻬��Ե��ˮƽ������һ�����Σ���a��b��c���������Ϸֱ���õ�����������Q����һ�������Ϊq������̽��ɷֱ��������������O��������ε���һ������d����������������ȷ���У�������
�⻬��Ե��ˮƽ������һ�����Σ���a��b��c���������Ϸֱ���õ�����������Q����һ�������Ϊq������̽��ɷֱ��������������O��������ε���һ������d����������������ȷ���У�������| A�� | q��d����еļ��ٶȷ�������O�������м��ٶȵķ�����ͬ | |
| B�� | q��d�������еĵ����ܴ�������O�������еĵ����� | |
| C�� | q��d�����ܵĵ糡����������O�����ܵĵ糡�� | |
| D�� | d��ĵ���һ����O��ĵ��Ƶ� |
���� ���ݿ��ض��ɺ͵糡���ĺϳɣ��Ƚϵ糡���Ĵ�С���糡������bdָ��d�㣬d��糡������ʸ���ϳɿ������b����ͬ���ݵ����Χ���Ƶ��ص�������Ƶĸߵ�
��� �⣺A���糡������odָ��d�㣬����q��d�������еļ��ٶȷ�������O�������еļ��ٶȷ�����ͬ����A��ȷ��
B���糡������odָ��d�㣬��O����Ƹߣ�����ͬһ��̽���+q��d�����O��ĵ�����С����B����
C���������εı߳�ΪL����O�㣺a��c�����ɶ�-q�ĵ糡����������b��q�ĵ糡����СΪ��${F}_{0}=\frac{kQq}{��\frac{\sqrt{2}}{2}L��^{2}}=\frac{2kQq}{{L}^{2}}$��
��d�㣺���ݿ��ض��ɺ����ĺϳɵã�����q���ܵĵ糡����СΪ��${F}_{d}=\frac{kQq}{{��\sqrt{2}L��}^{2}}+\frac{2kQq}{{L}^{2}}sin45��=��\frac{1}{2}+\sqrt{2}��\frac{kQq}{{L}^{2}}$
����ѧ֪ʶ�ã�FO��Fd����C����
D���糡������adָ��d�㣬��O����Ƹߣ�������ڵ���Խ�ߴ�������ԽС������ͬһ��̽���+q��d�����O��ĵ����ܴ�D��ȷ
��ѡ��AD
���� ���⿼��Ե糡���ӵ������Ӧ����������ȷ�������ʸ���ϳɷ���������Ƶĸߵ�

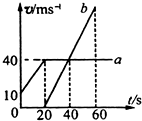
| A�� | a��b����ʱ������a�ļ��ٶȴ�������b�ļ��ٶ� | |
| B�� | 20��ĩ��a��b���������500m | |
| C�� | 40��ĩ��a��b��������ͬһλ�� | |
| D�� | 40��ĩ��a��b���������Զ |
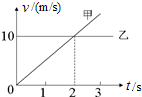 �����ʵ�����ң�ͬʱ��ͬһ�ص���ͬһ������ֱ���˶������ǵ�v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������
�����ʵ�����ң�ͬʱ��ͬһ�ص���ͬһ������ֱ���˶������ǵ�v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������| A�� | �ڵ�2��ĩ�ס��ҽ������� | B�� | �ڵ�2��ĩ�ס����ٶ���ͬ | ||
| C�� | ��ǰ2���ڣ���ƽ���ٶȱ��ҵĴ� | D�� | ����˵�������� |
| A�� | $\frac{{F}^{2}{t}^{2}}{2m}$��$\frac{{F}^{2}t}{2m}$ | B�� | $\frac{{F}^{2}{t}^{2}}{m}$��$\frac{{F}^{2}t}{m}$ | C�� | $\frac{{F}^{2}{t}^{2}}{2m}$��$\frac{{F}^{2}t}{m}$ | D�� | $\frac{{F}^{2}{t}^{2}}{m}$��$\frac{{F}^{2}t}{2m}$ |
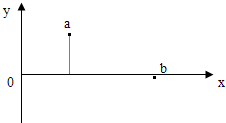 ������һ�����ҺᲨ��x�ᴫ����a��b���������㣨��ͼ��ʾ����������x�᷽���ϵľ���С��һ����������a������ߵ�ʱ��b��ǡ�þ�ƽ��λ�������˶�������ͼ��a��b֮�仭���������Σ��ֱ��ʾ��
������һ�����ҺᲨ��x�ᴫ����a��b���������㣨��ͼ��ʾ����������x�᷽���ϵľ���С��һ����������a������ߵ�ʱ��b��ǡ�þ�ƽ��λ�������˶�������ͼ��a��b֮�仭���������Σ��ֱ��ʾ��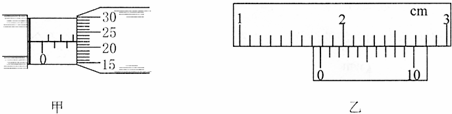
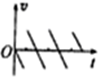
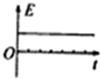
 ��ͼ��ʾ��һ����С����ijһ�߶��ɾ�ֹ�������䣬����淢����ײ����������˶��������ͷ�С��ʼ��ʱ������С������͵��������ʧ��������������ͼ������ȷ����С��λ��x���ٶ�v������Ek����е��E��ʱ��t��ϵ���ǣ�������
��ͼ��ʾ��һ����С����ijһ�߶��ɾ�ֹ�������䣬����淢����ײ����������˶��������ͷ�С��ʼ��ʱ������С������͵��������ʧ��������������ͼ������ȷ����С��λ��x���ٶ�v������Ek����е��E��ʱ��t��ϵ���ǣ�������