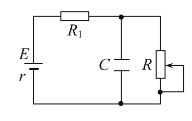
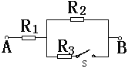
题目内容
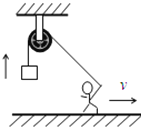
【题目】如图所示,一工人利用定滑轮和轻质细绳将货物提升到高处。已知该工人拉着绳的一端从滑轮的正下方水平向右匀速运动,速度大小恒为v,直至轻绳与竖直方向夹角为600。若滑轮的质量和摩擦阻力均不计,则该过程( )
A. 货物也是匀速上升
B. 绳子的拉力大于货物的重力
C. 末时刻货物的速度大小为![]()
D. 工人做的功等于货物动能的增量
【答案】B
【解析】
人的运动是合运动,其速度v沿绳子方向的分速度大小等于货物的速度,根据几何关系得出货物的速度,再分析其变化.然后根据牛顿第二定律求出绳的拉力T和物体的重力mg的关系.
由题意可知,将人的速度v沿绳子和垂直于绳方向分解,如图所示,沿绳的速度大小等于货物上升的速度大小,v货=vsinθ,θ随人向右运动逐渐变大,sinθ变大,若v不变,故货物运动的速度要变大,故A错误。
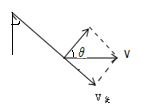
货物的加速度向上,由牛顿第二定律可知其合力向上,则绳的拉力T大于物体的重力mg,故B正确;末时刻货物的速度大小为v货=vsin600=![]() v,选项C错误;根据能量关系可知,工人做的功等于货物动能和重力势能的增量之和,D错误。故选B。
v,选项C错误;根据能量关系可知,工人做的功等于货物动能和重力势能的增量之和,D错误。故选B。

练习册系列答案
相关题目