题目内容
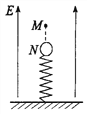
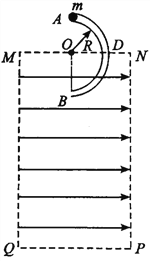
【题目】如图,矩形区域MNPQ内有水平向右的匀强电场,虚线框外为真空区域;半径R=lm、内壁光滑、内径很小的绝缘半圆管ADB固定在竖直平面内,直径AB垂直于水平虚线MN,圆心O在MN的中点,半圆管的一半处于电场中。一带正电的小球从半圆管的A点由静止开始滑入管内,到达B点时,小球对管壁的压力大小等于其重力的3倍。小球可视为质点,比荷q/m=l×10-2 C/kg,重力加速度g=10 m/s2。
(1)求小球在B点的速度大小v;
(2)求匀强电场的电场强度大小E;
(3)若小球能从MNPQ区域右边界NP离开电场,求该区域的高度HMQ和宽度的最小值LMN.
【答案】(1)2![]() m/s(2)1×103N/C(3)H≥4+2
m/s(2)1×103N/C(3)H≥4+2![]() m
m
【解析】(1)在B点,由牛顿第二定律: ![]()
解得![]()
(2)从A到B,由动能定理![]()
解得E=1×103N/C
(3)从B点滑出红,小球在竖直方向做自由落体运动;在水平方向的加速度恒定,先向左做匀减速运动,速度减为零后再向右做匀加速运动,水平方向:qE=max ax=g
竖直方向:ay=g
设向左减速的时间为t1,则有![]()
小球向左运动的最大距离为:x=![]() =R
=R
带入数据解得MNPQ区域的最小宽度为LMN=2R=2m
设向右加速的时间为t2,则有![]()
可得: ![]()
小球出电场时,下落的高度为![]() 解得h=3+2
解得h=3+2![]() m
m
故MNPQ区域的高度满足:H≥h+R=4+2![]() m
m

练习册系列答案
相关题目