题目内容
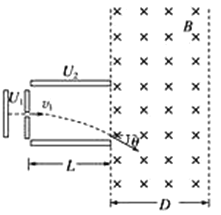
【题目】如图所示,一带电微粒质量为m=2.0×10-11kg、电荷量q=+1.0×10﹣5C,从静止开始经电压为U1=100V的电场加速后,水平进入两平行金属板间的偏转电场中,微粒射出电场时的偏转角θ=30°,并接着进入一个方向垂直纸面向里、宽度为D=34.6cm的匀强磁场区域.已知偏转电场中金属板长L=10cm,两板间距d=17.3cm,重力不计(![]() ≈1.73).求:
≈1.73).求:
(1)带电微粒进入偏转电场时的速率![]() ;
;
(2)偏转电场中两金属板间的电压U2;
(3)为使带电微粒不会由磁场右边射出,该匀强磁场的磁感应强度B至少多大?
【答案】(1)1.0×104m/s (2)200V (3)0.1T
【解析】
(1)带电微粒在电场中加速,由动能定理得:
qU1=![]()
代入数据解得:
![]()
(2)带电微粒在偏转电场中只受电场力作用,做类平抛运动.水平方向:
![]()
竖直方向:
![]()
![]()
tanθ=![]()
解得:
U2=![]()
代入数据解得:
U2=200V
(3)带电微粒进入磁场做匀速圆周运动,洛伦兹力提供向心力,微粒轨迹刚好与磁场右边界相切,设轨迹半径为R,由几何关系知:
D=R+Rcos60°
设微粒进入磁场时的速度为![]() ,则
,则
![]() =
=![]()
由牛顿第二定律得:
![]()
![]()
代入数据解得:
B=0.1T
若带电粒子不射出磁场,磁感应强度B至少为0.1T.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目