题目内容
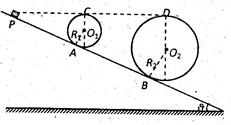
如图所示是游乐场中过山车的模型图，图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道，固定在倾角为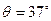
斜轨道面上的A、B两点，且两圆形轨道的最高点C、D均与P点平齐，圆形轨道与斜轨道之间圆滑连接，现使小车（视为质点）从P点以一定的初速度沿斜面向下运动，已知斜轨道面与小车间的动摩擦因数为
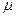= 1/6，g= 10m/s2，
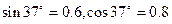。问：
（1）若小车恰能通过第一个圆形轨道韵最高点C，则在C点速度多大？PA距离多人？
（2）若小车恰好能通过第一个圆形轨道的最高点C，P点的初速度应为多大？
（3）若小车在P点的初速度为15m/s，则小车能否安全通过两个圆形轨道？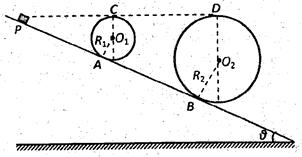
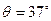斜轨道面上的A、B两点，且两圆形轨道的最高点C、D均与P点平齐，圆形轨道与斜轨道之间圆滑连接，现使小车（视为质点）从P点以一定的初速度沿斜面向下运动，已知斜轨道面与小车间的动摩擦因数为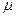= 1/6，g= 10m/s2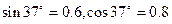，。问：（1）若小车恰能通过第一个圆形轨道韵最高点C，则在C点速度多大？PA距离多人？
（2）若小车恰好能通过第一个圆形轨道的最高点C，P点的初速度应为多大？
（3）若小车在P点的初速度为15m/s，则小车能否安全通过两个圆形轨道？
（1）
，
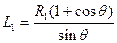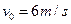
（2）
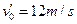
（3）能安全通过
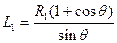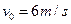
，（2）
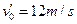
（3）能安全通过
（1）设小车经过C点时的临界速度为v1，则
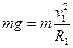（1分）
设P、A两点间距离为L1，由几何关系可得
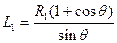（1分）
从P运动到C，根据动能定理，
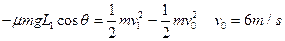（3分）
（2）设P、B两点间距离为L2，由几何关系可得
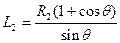（1分）
设小车能完全通过两个圆形轨道在D点的临界速度为v2，
则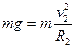
（1分）
设P点的初速度为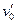
小车从P运动到D，根据动能定理，有
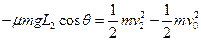
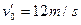（3分）
可知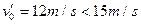
，能安全通过 （1分）
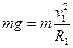（1分）设P、A两点间距离为L1，由几何关系可得
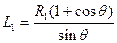（1分）从P运动到C，根据动能定理，
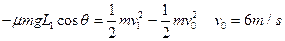（3分）（2）设P、B两点间距离为L2，由几何关系可得
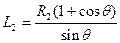（1分）设小车能完全通过两个圆形轨道在D点的临界速度为v2，
则
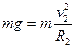（1分）设P点的初速度为
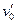小车从P运动到D，根据动能定理，有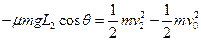 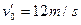（3分）可知
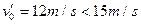，能安全通过 （1分）
练习册系列答案
相关题目
吸道方面的疾病，根据有关放射性知识可知，下列说法正确的是( )
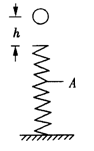
m2，若m1到达圆弧最低点a时（此时m2没有到达c点），绳子恰好与m1断开，则m1落地点离a点的水平距离是多少？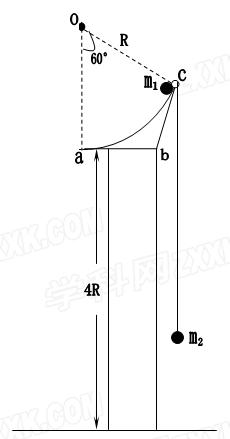
，小球2静止在最低点B，小球1从距地面某一高度沿斜轨道静止下滑，且于B位置与2相撞，球1和球2的对心碰撞时间极短且无机构能损失，碰后球1和球2的动量大小之比为1：2，方向相同，球2恰能到达C点，不计摩擦及空气阻力，重力加速度为g，求：
能进行检测的一种高科技产物，现代汽车的生产也有运用风洞技术进行检测的，如图所示是小丽所在兴趣小组设计的一个类似于风洞的实验装置，他们在桌面上放有许多大小不同的塑料球，这些塑料球的密度均为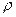
，用水平向左恒定的风作用在球上，使它们做匀加速运动（摩擦不计）。已知风对球的作用力F与球的最大横截面积S成正比，即F=kS，走为一常量。对塑料球来说，可以认为空间存在一个风力场，在该风力场中风力对球做功与路径无关。 （ ）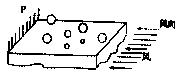
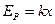
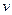表示，风力场中机械能守恒定律可写为
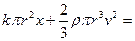恒量