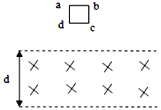题目内容
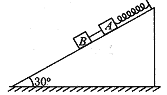
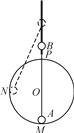
【题目】如图所示,A、B两小球质量均为m,A球位于半径为R的竖直光滑圆轨道内侧,B球穿过固定的光滑竖直长杆,杆和圆轨道在同一竖直平面内,杆的延长线过轨道圆心O.两球用轻质铰链与长为L(L>2R)的轻杆连接,连接两球的轻杆能随小球自由移动,M、N、P三点分别为圆轨道上最低点、圆心的等高点和最高点,重力加速度为g.
(1) 对A球施加一个始终沿圆轨道切向的推力,使其缓慢从M点移至N点,求A球在N点受到的推力大小F;
(2) 在M点给A球一个水平向左的初速度,A球沿圆轨道运动到最高点P时速度大小为v,求A球在M点时的初速度大小v0;
(3) 在(2)的情况下,若A球运动至M点时,B球的加速度大小为a,求此时圆轨道对A球的作用力大小FA.
【答案】(1) 2mg (2) ![]() (3)
(3) ![]()
【解析】试题分析:在N点,A、B和轻杆整体处于平衡状态,根据平衡条件可得A球在N点受到的推力大小;A球在M点、P点时,B球的速度都为零,A、B球和轻杆组成的系统在运动过程中满足机械能守恒定律即可求出A球在M点时的初速度大小;由牛顿第二定律可求出圆轨道对A球的作用力大小。
(1) 在N点,A、B和轻杆整体处于平衡状态,在竖直方向有:F-2mg=0
解得:F=2mg
(2) A球在M点、P点时,B球的速度都为零
A、B球和轻杆组成的系统在运动过程中满足机械能守恒定律,则
![]()
解得: ![]()
(3) 此时B球有向上的加速度a,设杆对B球支持力为F0,由牛顿第二定律有
F0-mg=ma
A球此时受到重力、轨道竖直向上的支持力和轻杆竖直向下的压力,同理有
![]()
解得: ![]()

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】如图为某放射源放出的三种射线在匀强电场或匀强磁场中的轨迹示意图,已知三种射线的性质如下表:

射线名称 | 本质 | 电荷数 | 质量数 | 速度 |
α射线 | 氦原子核 | 2 | 4 | 0.9c |
β射线 | 电子 | -1 | 0 | 0.99c |
γ射线 | 光子 | 0 | 0 | c |
以下判断正确的是:
A. 若是在匀强磁场中,磁场垂直纸面向里,且①为α射线
B. 若是在匀强磁场中,磁场垂直纸面向外,且③为α射线
C. 若是在匀强电场中,电场方向水平向右,且③为α射线
D. 若是在匀强电场中,电场方向水平向左,且①为α射线