Question

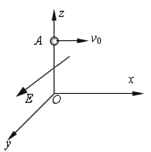
【题目】如图所示，一轻质弹簧的上端固定在倾角为30°的光滑斜面顶部，下端栓接小物块A，A通过一段细线与小物块B相连，系统静止时B恰位于斜面的中点。将细线烧断，发现当B运动到斜面底端时，A刚好第三次到达最高点。已知B的质量m=2kg，弹簧的劲度系数k=l00N／m，斜面长为L=5m，且始终保持静止状态，重力加速度g=l0m/s2。

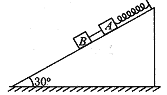
(i)试证明小物块A做简谐运动；

(ii)求小物块A振动的振幅和周期。

Answer 1

【答案】：（i）证明小物块A做简谐运动见解析；
（ii）0.1m； 0.4s．

【解析】（i）烧断细线后A向上运动，受力平衡时，设弹簧的伸长量为x0，则：kx0-mAgsin30°=0 ①
选A的平衡位置处为坐标原点，沿斜面向下为正方向建立坐标系，用x表示A离开平衡位置的位移．当A运动到平衡位置下x位置时，物块A受到的合力为：
F0=mAgsin30°-k（x-x0） ②
联立①②得：F0=-kx，可知A受到的合外力总是与物块的位移成反比，所以A做简谐振动．
（ii）开始时AB组成的系统静止时，设弹簧的伸长量为x1，根据胡克定律有：
kx1-（mA+mB）gsin30°=0 ③
所以：
烧断细线后A从此位置开始向上运动，到达平衡位置运动的距离为物块A的振幅，则：
A=x1x0＝
代入数据得：A=0.1m
烧断细线后B向下做匀加速直线运动，则：mBgsin30°=mBa
设B到达斜面底端的时间为t，则：

A向上运动经过周期第一次到达最高点，则第三次到达最高点的时间：t=2.5T
代入数据联立得：T=0.4s